Which type of equation to use in the curve fitting tool in Matlab?-CodePudding

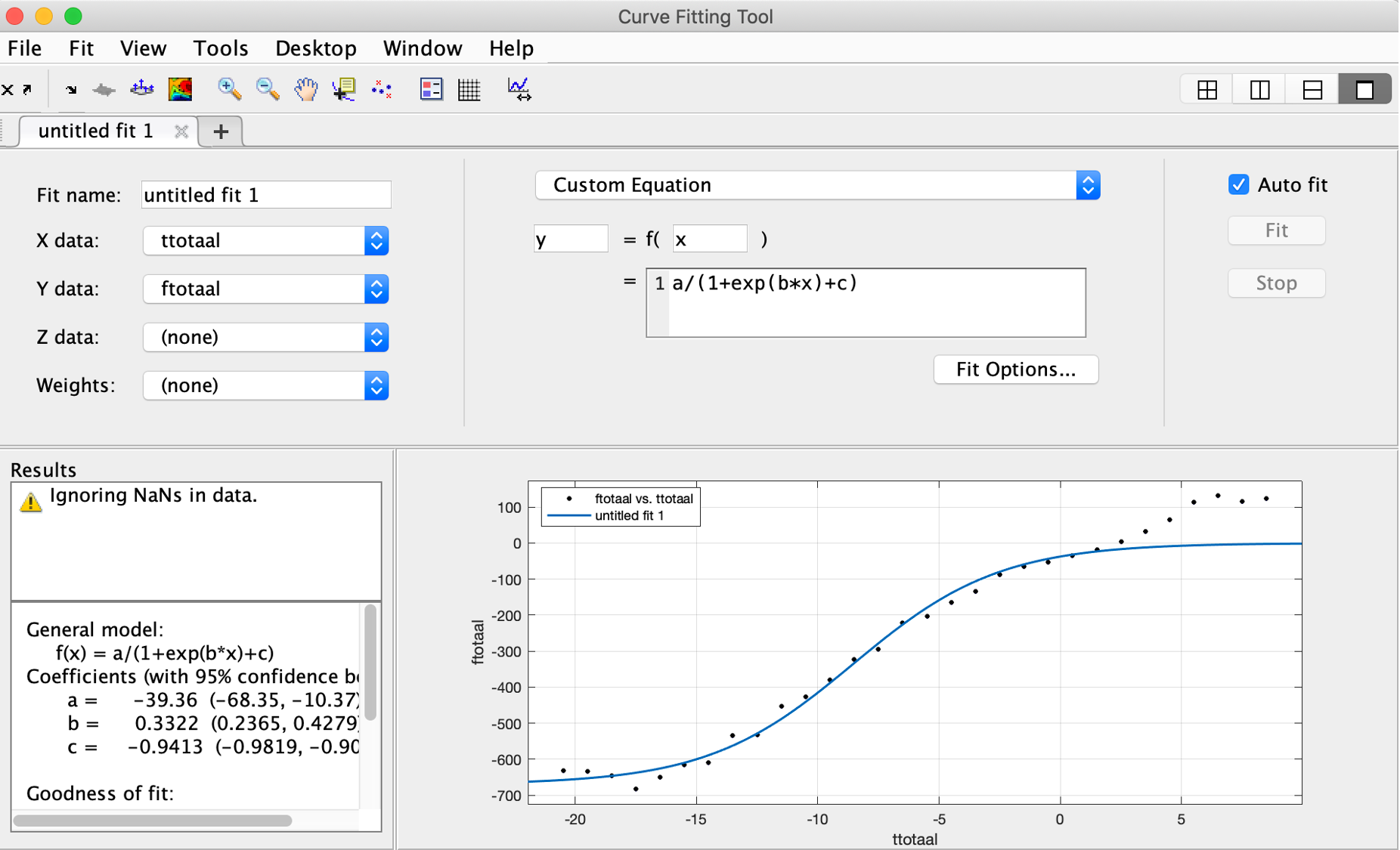
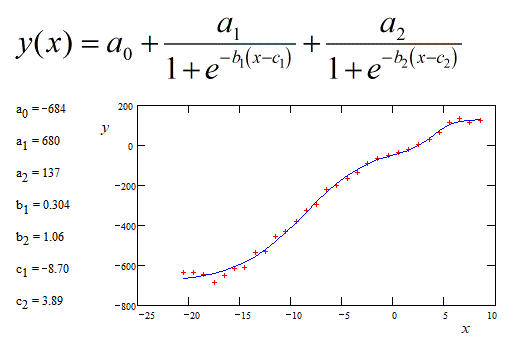I have some data points and I want to fit a custom equation to that curve. The data are as follows:

-20.5   -632.8475722
-19.5   -633.3214772
-18.5   -646.6016049
-17.5   -683.4637841
-16.5   -649.8121364
-15.5   -616.4297769
-14.5   -609.9639983
-13.5   -534.5818772
-12.5   -532.2347152
-11.5   -452.9222271
-10.5   -427.6525318
-9.5    -380.3710984
-8.5    -322.5516672
-7.5    -294.1208624
-6.5    -222.1675481
-5.5    -202.2179342
-4.5    -165.122709
-3.5    -134.827559
-2.5    -88.25392126
-1.5    -66.0446787
-0.5    -52.03853651
0.5 -35.01795243
1.5 -18.27307888
2.5 4.200002613
3.5 31.46742774
4.5 65.02174186
5.5 113.4098161
6.5 132.8355363
7.5 115.0080076
8.5 124.3832919

It looks to me like a sigmoidal-type function, but I cannot find the correct custom-type equation to fit the data. I have tried the following, but it misses the upper values. Which type of equation can I use?

Thanks

CodePudding user response：

A simple linear fitting (blue) is better than your logistic fitting (lime) :

This is due to the model y(x)=a / (1 exp(b * x) c)

For this model y(x) tends to 0 for large x which is not consistent with the data : Obviously y(x) is larger than 0 for large x.

Instead of the three parameters logistic function, try the four parameters logistic function : y(x) = K a / ( 1 exp(b * x) c)

Even more, the shape of the points makes think to a double logistic y(x) = K a / (1 exp(b * x) c) A / (1 exp(B * x) C) but too many parameters makes difficult the non-linear fitting process.

Or on an equivalent form of double logistic function (written with different symbols) :

Nevertheless I agree with a large part of the comment from Cris Luengo to the main question.