The problem is to find the optimum(maximum) value of x3 in range of (-8e-4 to 2e-4) by varying kst,x1,x5 and xo)
x5=5 %Input 2 (Input 2 is a state variable and could vary in range of 4 to 15 while performing
optimization)
kst=1 %Input 3 (Input 3 is in terms of rate constant, it could vary from 0.1 to 2)
xo=4 %Input 4 (Input 4 is a state variable and could vary in range of 4 to 10)
x1=1e-7 %Input 1 could vary from 1e-9 to 1e-6
- Script file
function rest = Scrpt1(t,X)
x2 = X(1);
x3 = X(2);
%Parameters
if t<15
x1 = 1e-7; %Input 1 could vary from 1e-9 to 1e-6
else x1 = 0;
end
x5=5 %Input 2 (Input 2 is a state variable and could vary in range of 4 to 15 while performing optimization)
kst=1 %Input 3 (Input 3 is in terms of rate constant, it could vary from 0.1 to 2)
xo=4 %Input 4 (Input 4 is a state variable and could vary in range of 4 to 10)
k1 = 6e7;
km1 = 0.20;
km4 = 0.003;
k3 = 2500.00;
k4 = km4/9;
km3 = km1;
LAP=1.5
% Differential equations
dx2dt = km1*x3 km3*LAP - k1*x1*x2 km4*x3 - k4*x2;
dx3dt = k1*x1*x2 - km1*(x3 x5 xo) - k3*x3*kst;
rest = [dx2dt; dx3dt];
end
- Function file for ODE solution
options = odeset('InitialStep',0.0001,'RelTol',1e-09);
[T,Y]=ode15s(@Scrpt1,[0 60],[9e-13,0],options);
X3= Y(:,2);
plot(T,X3)
How to use fmincon or any other optimization solver for this to solve the mentioned optimization problem of finding maximum value of x3. For which values of x5,kst,xo,x1 we get maximum x3?
CodePudding user response:
First you must add the values you want wo optimie as parameters of your coupled diffrential equations:
function rest = Scrpt1(t,X,X_opt)
x5=X_opt(1);
kst=X_opt(2);
xo=X_opt(3);
x1=X_opt(4);
x2 = X(1);
x3 = X(2);
%Parameters
if t>=15
x1 = 0;
end
k1 = 6e7;
km1 = 0.20;
km4 = 0.003;
k3 = 2500.00;
k4 = km4/9;
km3 = km1;
LAP=1.5;
% Differential equations
dx2dt = km1*x3 km3*LAP - k1*x1*x2 km4*x3 - k4*x2;
dx3dt = k1*x1*x2 - km1*(x3 x5 xo) - k3*x3*kst;
rest = [dx2dt; dx3dt];
end
then you have to wirte a wrapper function you want to minimize. Because you want to maxmize x3 you have to add an minus to your objective value.
function max_X3=fun(X_opt)
tspan=[0 60];
y0=[9e-13,0];
options = odeset('InitialStep',0.0001,'RelTol',1e-09);
[~,y] = ode15s(@(t,y) Scrpt1(t,y,X_opt), tspan, y0,options);
max_X3=-max(y(:,2));
end
Finally you can use fmincon like this:
% x5, kst, xo, x1
initial_search_point=[5, 1, 4, 1e-7]
lower_bounds=[4, 0.1, 4, 1e-9]
upper_bounds=[15, 2, 10, 1e-6]
fmincon(@fun,initial_search_point,[],[],[],[], lower_bounds,upper_bounds)
CodePudding user response:
import numpy as np
from gekko import GEKKO
n = 121; t = np.linspace(0,60,n)
m = GEKKO(remote=False)
m.time = t
k1 = 6e7; km1 = 0.20; km4 = 0.003;
k3 = 2500.00; k4 = km4/9;
km3 = km1; LAP=1.5
x5 = m.FV(value=5,lb=4,ub=15); x5.STATUS = 1
kst = m.FV(value=1,lb=0.1,ub=2); kst.STATUS = 1
xo = m.FV(value=4,lb=4,ub=10); xo.STATUS = 1
x1 = m.FV(value=[1e-17 if t[i]<15 else 0 for i in range(n)],\
lb=1e-9,ub=1e-6)
x2,x3 = m.Array(m.Var,2)
x3.value = -0.00032
x3.lower = -8e-4
x3.upper = 2e-4
m.Equations([x2.dt()==km1*x3 km3*LAP-k1*x1*x2 km4*x3-k4*x2,
x3.dt()==k1*x1*x2-km1*(x3 x5 xo)-k3*x3*kst])
m.Maximize(x3)
m.options.SOLVER = 1
m.options.IMODE = 6
m.solve()
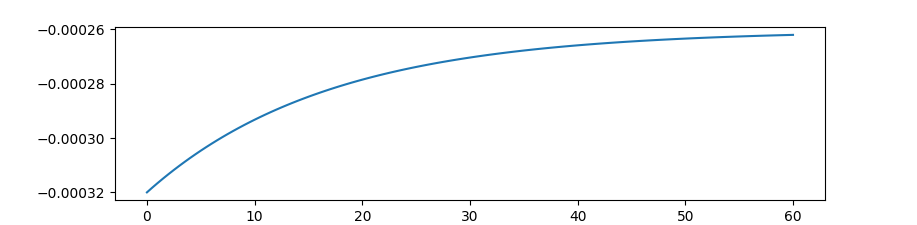
import matplotlib.pyplot as plt
plt.plot(m.time,x3)
plt.show()
The initial condition for x2 and x3 are not defined.
Number of state variables: 483
Number of total equations: - 480
Number of slack variables: - 0
---------------------------------------
Degrees of freedom : 3
----------------------------------------------
Dynamic Control with APOPT Solver
----------------------------------------------
Iter Objective Convergence
0 4.99217E 02 2.99935E-01
1 6.07645E-02 4.31439E-05
2 3.25294E-02 3.04712E-05
3 3.41027E-02 8.96081E-05
4 3.31615E-02 2.48287E-06
5 3.31615E-02 2.22045E-16
6 3.31615E-02 2.22045E-16
Successful solution
---------------------------------------------------
Solver : APOPT (v1.0)
Solution time : 2.189999999245629E-002 sec
Objective : 3.316154172805905E-002
Successful solution
---------------------------------------------------