Closed. This question needs
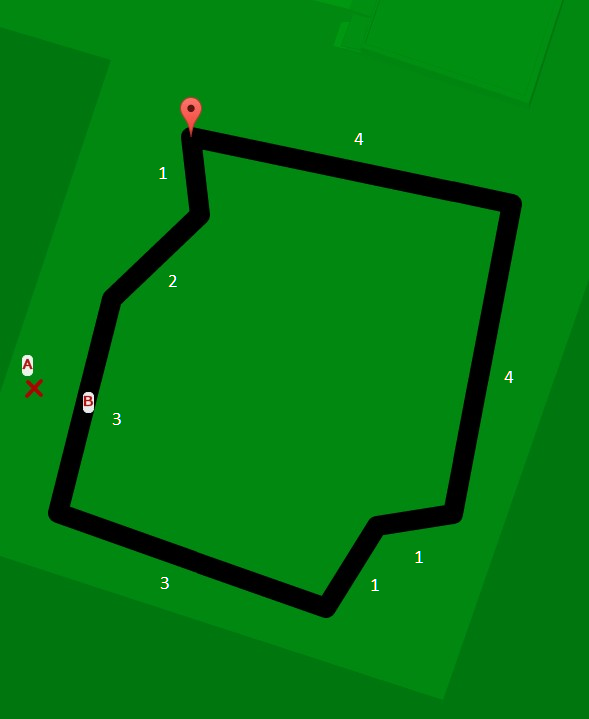
Then you have to convert it to a binary tree
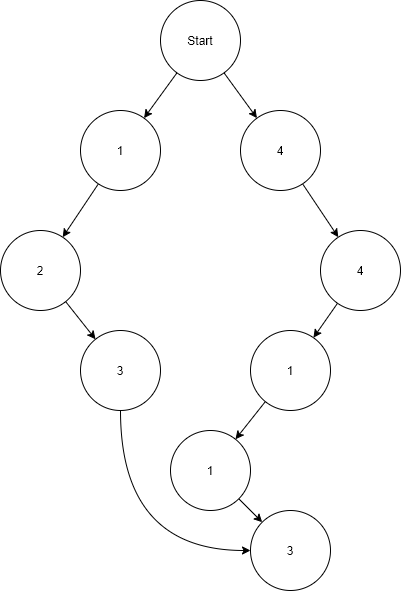
Now you can find the shortest route between nodes as required. (I am not sure where the start and end is, so I assumed the pin to be the start node)
CodePudding user response:
If typical paths that your program is expected to handle have comparatively few segments then your best bet is probably to just brute force it: compute the nearest point on each segment via the standard geometric formula, and choose the one that is overall closest. You would want to test to be sure, but I estimate that you would need to be dealing with paths having at least several dozen segments before a BSP or any other variety of search tree would provide a significant performance advantage -- and that ignores the cost of building the tree in the first place.
Additionally, the brute-force approach is both memory-efficient and code-efficient, and the key computation involved is going to be needed for most other approaches too. Thus, it seems a no-brainer to implement the brute-force linear search, and to attempt something more complicated only if that isn't fast enough.
Note well, too, that an efficient tree-based approach to the problem would probably use the tree not to find a specific point, but rather to determine a small number (ideally 1) of segments that might contain the wanted point. You would then use the standard formula to identify the wanted specific point, much the same as in the brute-force version.
Note also that in all cases, you need to account for
- ties, and
- cases where the nearest point on a given segment is one of the endoints.
