How to Position Objects With Same Distances-CodePudding

I am coding a game in Unity that number of your soldiers are increasing/decreasing by some triggers. I want to position my soldier objects like a full circle, so they will always be near each other(like same distances) even if their number is increasing or decreasing. How can I manage this?

CodePudding user response：

Supposing you are working in the horizontal plane, you can define you much rotation for each of your soldiers, and the find that point in the plane converting cartesian coordinates (x, y) into polar ones (R, fi), add theta to fi and then convert back to cartesian:

// Rotate B around A by angle theta
private (float x, float y) Rotate(
  (float x, float y) A, 
  (float x, float y) B, 
  float theta) {
  
  float fi = Math.Atan2(B.y - A.y, B.x - A.x)   theta;
  float R = Math.Sqrt((A.y - B.y) * (A.y - B.y)   (A.x - B.x) * (A.x - B.x));

  return (A.x   R * Math.Cos(fi), A.y   R * Math.Sin(fi));
}

Another option that does exactly the same thing, but not using polar coords:

// Rotate B around A by angle theta clockwise
private (float x, float y) Rotate(
      (float x, float y) A,
      (float x, float y) B,
      float theta)
{
        float s = Math.Sin(theta);
        float c = Math.Cos(theta);

        // translate point back to origin:
        B.x -= A.x;
        B.y -= A.y;

        // rotate point clockwise
        float xnew = B.x * c - B.y * s;
        float ynew = B.x * s   B.y * c;

        // translate point back:
        B.x = xnew   A.x;
        B.y = ynew   A.y;

        return B;
}

If you want your soldiers equally distributed in a circle you would need to calcualte the rotation angle of each just with float angle = 360 / numSoldiers;.

If your game is in 3d and you are working in the floor plane (XZ) you can change the .ys by .zs in the code.

You can also check how the algorithms work in a simple unity project cubes or in a console c# app to understand them and to check how they just perform the rotation of a vector's end point around its origin to return the rotated point. I think that is what you would need to find the points of interest for the position of your soldiers.

CodePudding user response：

You can start with some simple relatively ordered distribution of positions and by applying a dynamical system approach/gradient decent type iteration, you can let the positions converge to a much more structured pattern. I wrote such implementation in python, it is in vectorized form, but I also added an equivalent function with for loops, to illustrate the structure of the function. The final ordered pattern is inspired by the stable equilibrium position that a bunch of discs of same radius r would form if they are hold by springs, one for every two of them. To ease up the computations, I squared the spring tensions, thus avoiding square roots, so not exactly like the typical physics model, but close to it.

import numpy as np
import matplotlib.pyplot as plt

def Grad(pos, r):
    Dq = - pos[:, :, np.newaxis]   pos[:, np.newaxis, :] 
    D = Dq[0,:,:]*Dq[0,:,:]   Dq[1,:,:]*Dq[1,:,:]   np.identity(Dq.shape[1]) 
    Dq = (1 - r**2 / D) * Dq
    return - Dq.sum(axis=2)

def Grad_flow(q_, r, step):
    Q = q_
    n_iter = 0
    while True:
        n_iter = n_iter   1 # you can count the number of iterations needed to reach the equilibrium
        Q_prev = Q
        Q = Q - step * Grad(Q, r) 
        if np.sum(np.abs((Q.T).dot(Q) - (Q_prev.T).dot(Q_prev))) < 1e-5:
            return Q

'''
Test:
'''

p = np.array([[-3, 3], [-1, 3], [1,3], [3,3],
              [-3, 1], [-1, 1], [1,1], [3,1],
              [-3,-1], [-1,-1], [1,-1], [3,-1],
              [-3,-3], [-1, -3], [1, -3], [3,-3], 
              [-2, 1], [-1,2],[2,-2], [-2,-2], 
              [2,2], [2,0]]).T
r = 0.5
step = 0.01
q = Grad_flow(p, r, step)

'''
Plot:
'''

fig, axs = plt.subplots(1,1)
axs.set_aspect('equal')

axs.plot(q[0,:], q[1,:], 'ro')
axs.plot(p[0,:], p[1,:], 'bo')

plt.grid()
plt.show()

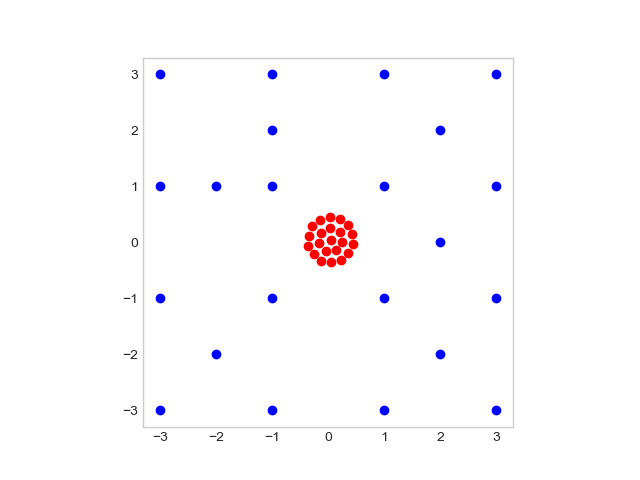
You start from the blue positions and you make them converge to the red positions:

Here is the loop version of the Grad function:

def Grad(pos, r):
    grad = np.zeros(pos.shape, dtype=float)
    for i in range(pos.shape[1]):
        for j in range(pos.shape[1]):
            if not i==j:
                d_pos_0 = pos[0, i] - pos[0, j]
                d_pos_1 = pos[1, i] - pos[1, j]
                m = d_pos_0*d_pos_0   d_pos_1*d_pos_1
                m = 1 - r*r / m
                grad[0, i] = grad[0, i]     m * d_pos_0
                grad[1, i] = grad[1, i]     m * d_pos_1
    return grad

Of course, all of this is a bit heuristic and I cannot promise full generality, so you have to play and select the parameters r which is half-distance between positions, iteration step-size step, the initial position p and so on.