How to create an equally spaced grid of a diamond shaped area-CodePudding

I am trying to construct an equally spaced grid of points within an area that resembles an irregular diamond or rhombus. The border of this diamond is given by the following lists:

xlim = list(np.linspace(0,1/4*(np.sqrt(3) 1), num=56))   list(np.linspace(1/4*(np.sqrt(3) 1),np.sqrt(3)/2, num=20))   \
list(np.linspace(np.sqrt(3)/2, 1/4*(np.sqrt(3) 1), num=20))   list(np.linspace( 1/4*(np.sqrt(3) 1),0, num=56))

ylim = list(np.linspace(0, np.sqrt(3)/4, num=56))   list(np.linspace(np.sqrt(3)/4,0, num=20))  \
list(np.linspace(0, -np.sqrt(3)/4,num=20))   list(np.linspace(-np.sqrt(3)/4,0, num=56))

Then I created border list that holds a tuple with the coordinates of the perimeter:

border = []

for i in range(len(xlim)):
    border.append((xlim[i],ylim[i]))

You can check that by plotting the xlim and ylim arrays we get the polygon shape below .

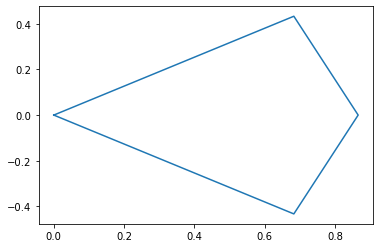I am trying to create an equally spaced grid inside of this polygon and including the borders and this is what I have done so far:


width = np.linspace(0,np.sqrt(3)/2,20)
kgrid = []

for i in range(0,len(width)):
    for j in range(0,len(width)):
        
        x = width[i]
        y = width[j]
        
        if (x,y) in border:
            
            continue
            
        else:
            kgrid.append([x,y])

Kgrid would be my resulting list with the tuples of the x and y coordinates of the equally spaced dots, however, I get the entire square of length and width sqrt(3)/2 instead of the grid within the diamond only.

I am not entirely sure what I am doing wrong so any instruction or tips towards the right direction is going to be helpful for me.

CodePudding user response：

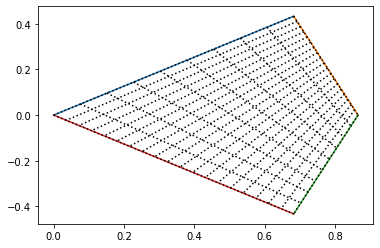
IIUC you want to get a grid of lines joining the opposite sides.

For this you can keep the coordinates of the four sides separate and join the evenly spaced points using loops:

n1 = 10 # number of blue -> green linew
n2 = 20 # number of orange -> red lines

faces = [ # blue
         (np.linspace(0,1/4*(np.sqrt(3) 1), num=n1), np.linspace(0, np.sqrt(3)/4, num=n1)),
          # orange
         (np.linspace(1/4*(np.sqrt(3) 1),np.sqrt(3)/2, num=n2), np.linspace(np.sqrt(3)/4,0, num=n2)),
          # green
         (np.linspace(np.sqrt(3)/2, 1/4*(np.sqrt(3) 1), num=n1), np.linspace(0, -np.sqrt(3)/4,num=n1)),
          # red
         (np.linspace( 1/4*(np.sqrt(3) 1),0, num=n2), np.linspace(-np.sqrt(3)/4,0, num=n2)),
        ]

ax = plt.subplot()
for face in faces:
    ax.plot(face[0], face[1])

for i in range(2):
    x1 = faces[i][0]
    x2 = faces[i 2][0][::-1]
    y1 = faces[i][1]
    y2 = faces[i 2][1][::-1]
    
    X = list(zip(x1, x2))
    Y = list(zip(y1, y2))
    
    for x, y in zip(X, Y):
        ax.plot(x, y, c='k', ls=':')

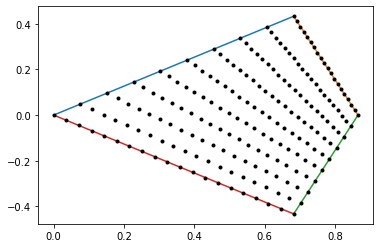
same with points:

n1 = 10
n2 = 20

faces = [(np.linspace(0,1/4*(np.sqrt(3) 1), num=n1), np.linspace(0, np.sqrt(3)/4, num=n1)),
         (np.linspace(1/4*(np.sqrt(3) 1),np.sqrt(3)/2, num=n2), np.linspace(np.sqrt(3)/4,0, num=n2)),
         (np.linspace(np.sqrt(3)/2, 1/4*(np.sqrt(3) 1), num=n1), np.linspace(0, -np.sqrt(3)/4,num=n1)),
         (np.linspace( 1/4*(np.sqrt(3) 1),0, num=n2), np.linspace(-np.sqrt(3)/4,0, num=n2)),
        ]

ax = plt.subplot()
for face in faces:
    ax.plot(face[0], face[1])

i = 0
    
x1 = faces[i][0]
x2 = faces[i 2][0][::-1]
y1 = faces[i][1]
y2 = faces[i 2][1][::-1]
    
X = list(zip(x1, x2))
Y = list(zip(y1, y2))

for x, y in zip(X, Y):
    xs = np.linspace(*x, num=20)
    ys = np.linspace(*y, num=20)
    ax.plot(xs, ys, c='k', ls='', marker='.')

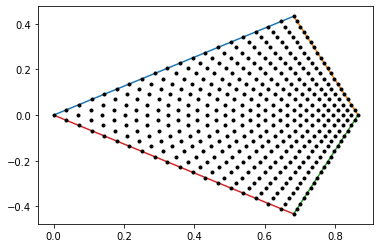
same with n1 = 20 and n2 = 20:

CodePudding user response：

My approach would be to get a gird covering your diamond and then remove the points outside of it.

First I put your points in an array and calculate the center

import numpy as np
import matplotlib.pyplot as plt
import functools

arr = np.array([[ 0.       ,  0.       ],
                [ 0.6830127, -0.4330127],
                [ 0.8660254,  0.       ],
                [ 0.6830127,  0.4330127],
                [ 0.       ,  0.       ]
               ])

center = np.mean(arr, axis=0)

Now I create a grid covering the diamond.

x = np.arange(min(arr[:,0]), max(arr[:,0]) 0.025, 0.025)
y = np.arange(min(arr[:,1]), max(arr[:,1]) 0.025, 0.025)
a,b = np.meshgrid(x,y)
points = np.stack([a.reshape(-1),b.reshape(-1)]).T

And finally I filter by being inside your diamond using the typical numpy approach of masking. That means I first create a true/false array being true where the points are that I want to keep and false otherwise and then apply it to the points.

def normal(a,b):
    v = b-a
    n = np.array([v[1], -v[0]])
    #normal needs to point out
    if (center-a)@n > 0:
         n *= -1
    return n

mask = functools.reduce(np.logical_and, [((points-a)@normal(a, b)) < 0 for a,b in zip(arr[:-1], arr[1:])])
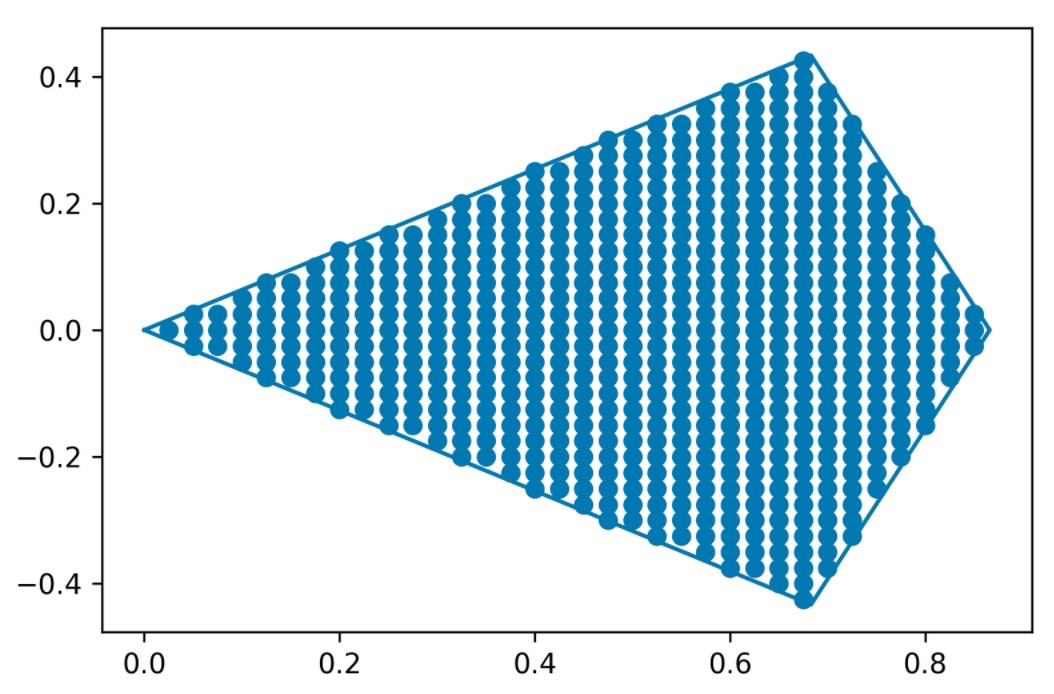
plt.plot(arr[:,0],arr[:,1])
plt.gca().set_aspect('equal')
plt.scatter(points[mask][:,0], points[mask][:,1])

Obviously your points are given as points[mask].