Scipy Lagrange division by zero-CodePudding

I am trying to interpolate a set of ordered pairs using Numpy's Lagrange Interpolation; I have done this before without incident. This time, however, I keep getting "Division by zero error" and the interpolating polynomial comes out with infinite coefficientes. I am aware data points must not be repeated due to the internal workings of Lagrange's Method, and they are not repeated.

Here is my code and the offending ordered pair, in numpy vector format. Code:

x = out["x"].round(decimals=3)
x = np.array(x)
y = out["y"].round(decimals=3)
y = np.array(y)
print(x)
print(y)
pol = lagrange(x,y)
print(pol)

Ordered pair:

[273.324 285.579 309.292 279.573 297.427 290.681 276.621 293.586 283.463
 284.674 273.904 288.064 280.125 294.269 288.51  285.898 273.419 273.023
 281.754 281.546 283.21  303.399 297.392 293.359 306.404 356.285 302.487
 280.586 299.487 302.487]
[ 0.     5.414  6.202  0.     9.331 11.52   0.    10.495  5.439  4.709
  0.     4.916  0.    10.508  6.736  5.25   0.     0.     6.53   4.305
  5.124  6.753 10.175 10.545  5.98   9.147 11.137  0.     8.764  9.57 ]

Lots of thanks in advance.

CodePudding user response：

Why Lagrange Interpolation did not work for you.

You have the value 302.487 twice in your array x. I.e. you did repeat it.

Why Lagrange Interpolation is not what you want.

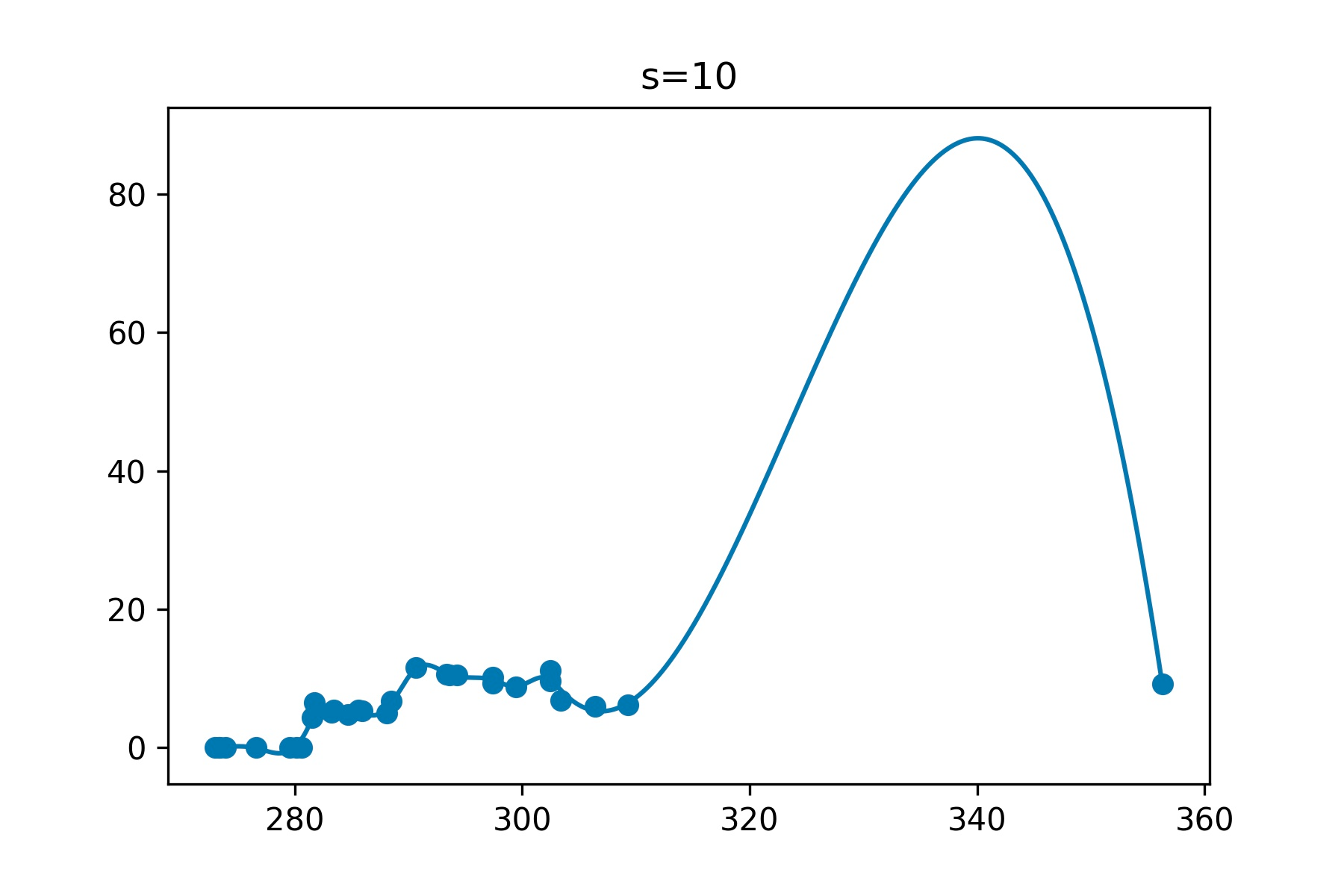
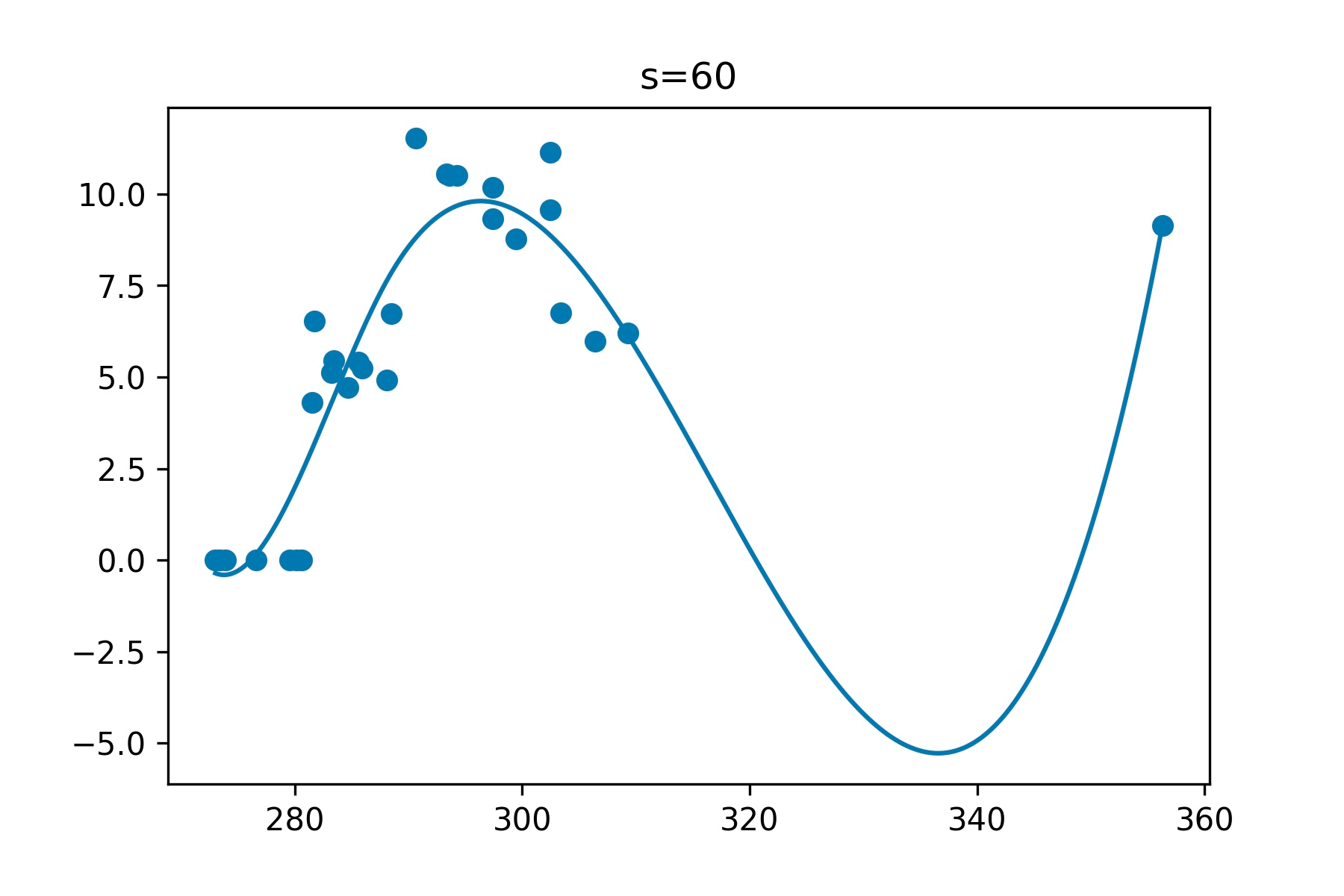
As Tim Roberts pointed out Lagrange interpolation is really not made for 20 points. The problem is that polynomials of high degree tend to overfit. Check out the following example from the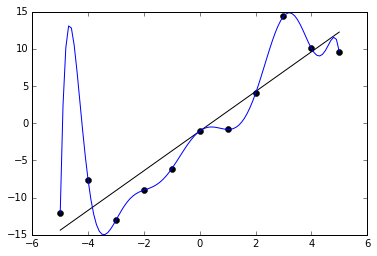

Figure 2. Noisy (roughly linear) data is fitted to a linear function and a polynomial function. Although the polynomial function is a perfect fit, the linear function can be expected to generalize better: if the two functions were used to extrapolate beyond the fitted data, the linear function should make better predictions.

Alternative Regression

There are at least two valid alternatives. One of them being what is recommended in the wikipedia article. If you know what type of function your data is ruffly coming from use regression to fit a function of that type to the data. In the case of the example above thats a linear function. If you want to do that check out