How do you rectify a 3D planar polygon?-CodePudding

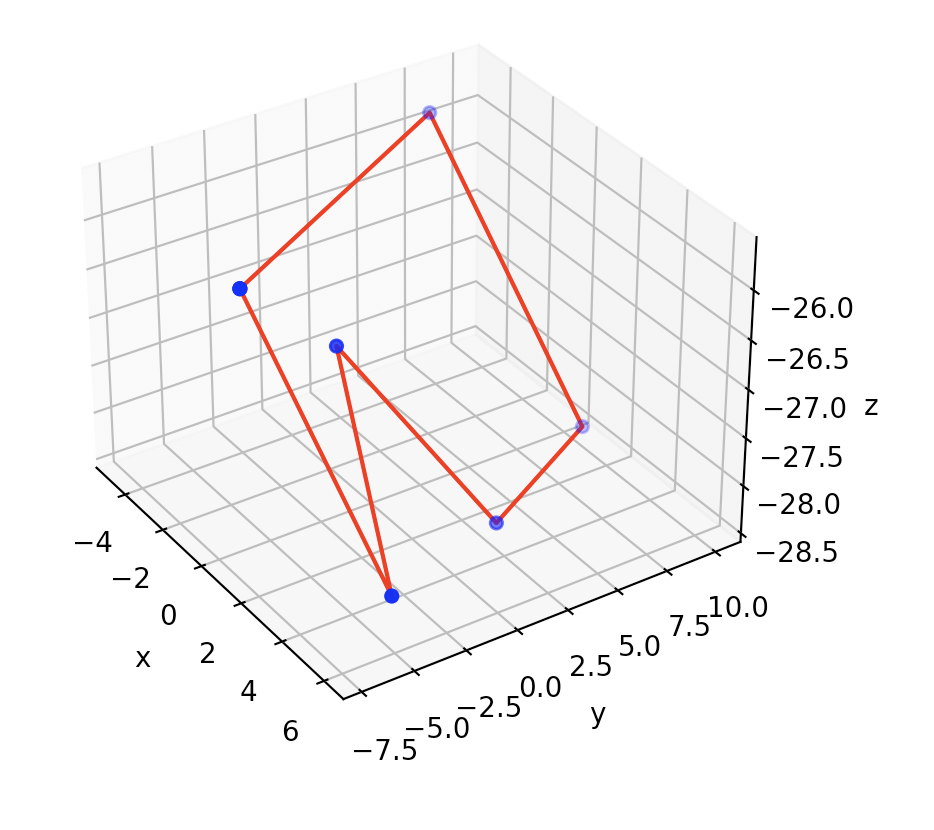
I have a 3D planar (all vertices lie in some plane) polygon with vertices: [(x1, y1, z1) ... (x1, y1, z1)].

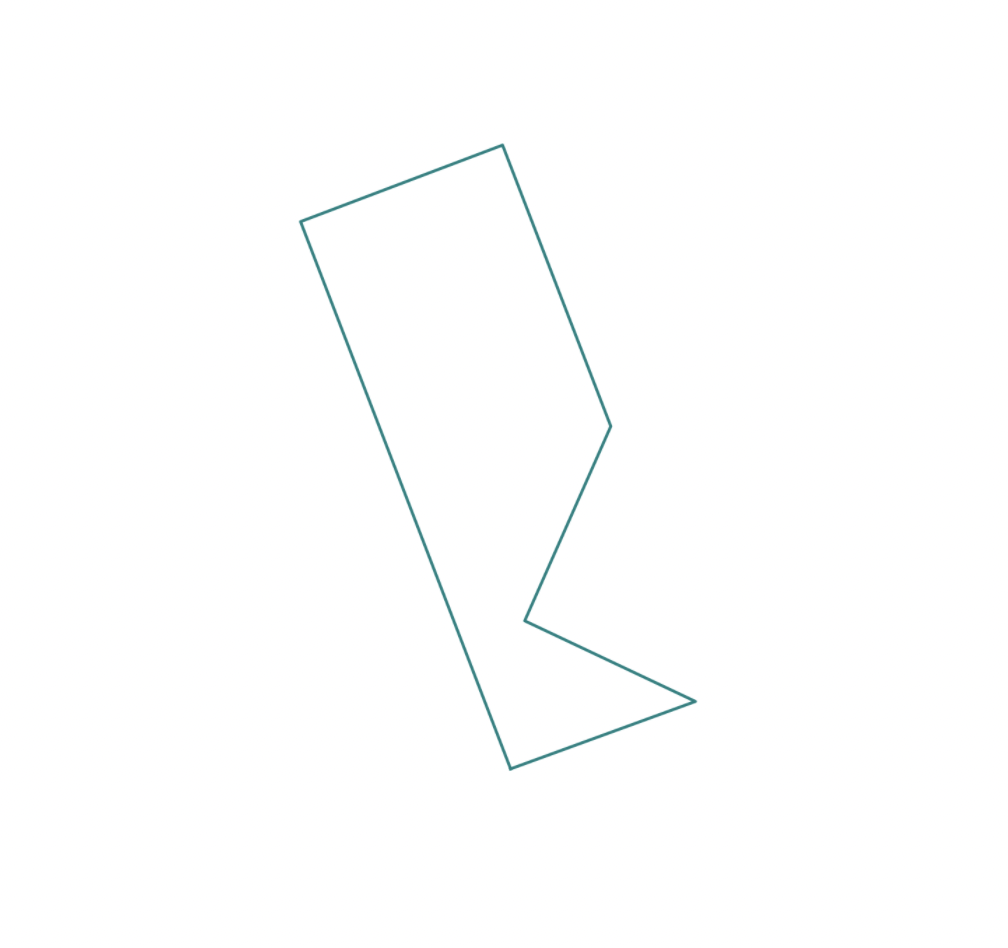
I would like to transform this polygon so that I'm viewing it orthographically (as if I'm looking at it straight on).

How can this be done in Python?

CodePudding user response：

I assume you have no information except for vertex coordinates.

Take three non-collinear (perhaps consequent) vertices C, A, B. Calculate normalized vector (divide by vector length)

b = (B - A) / |B - A|

then normal vector (using vector/cross multiplication)

N = b.cross.(A-C) and normalize it
un = N / |N|

and another unit vector in polygon plane

v = b.cross.n

Now we want find such matrix of affine transformations, that transforms vertex A into point (0,0,0), edge AB will be collinear with OX axis, normal will be collinear with OZ axis, vector q will be collinear with OY axis. This all means that rotated polygon will lie in OXY plane.

Mathematically: points A, u=A b, v=A q, n=A un should be transformed in quadruplet (0,0,0), (1,0,0), (0,1,0), (0,0,1). In matrix form

      [Ax ux vx nx]   [0 1 0 0]
 M *  [Ay uy vy ny] = [0 0 1 0]
      [Az uz vz nz]   [0 0 0 1]
      [1  1  1  1 ]   [1 1 1 1]

  M * S = D

Using matrix inverse

  M * S * Sinv = D * Sinv

and finally

  M = D * Sinv

So calculate matrix M and multiply it with every vertex coordinates. New coordinates should have zero Z-component (or very small due to numerical errors).

You can perform all described operations with numpy library with a little code

Example with specific data

Quick-made implementation in plain Python for reference

import math
def calcMatrix(ax, bx, cx, ay, by, cy, az, bz, cz):
    ux, uy, uz = bx - ax, by - ay, bz - az
    mag = math.sqrt(ux*ux uy*uy  uz*uz)
    ux, uy, uz = ux / mag, uy / mag, uz / mag
    Cx, Cy, Cz = ax - cx, ay - cy, az - cz
    nx, ny, nz = uy * Cz - uz * Cy, uz * Cx - ux * Cz, ux * Cy - uy * Cx
    mag = math.sqrt(nx*nx ny*ny nz*nz)
    nx, ny, nz = nx / mag, ny / mag, nz / mag
    vx, vy, vz = uy * nz - uz * ny, uz * nx - ux * nz, ux * ny - uy * nx
    denom = 1.0 / (ux*ux uy*uy   uz*uz)
    M = [[0.0]*4 for _ in range(4)]
    M[3][3] = 1.0

    M[0][0] = denom*(ux)
    M[0][1] = denom*(uy)
    M[0][2] = denom*(uz)
    M[0][3] = denom*(-ax*ux-ay*uy az*uz)

    M[1][0] = denom*(vx)
    M[1][1] = denom*(vy)
    M[1][2] = denom*(vz)
    M[1][3] = -denom*(ax*vx-ay*vy az*vz)

    M[2][0] = denom*(nx)
    M[2][1] = denom*(ny)
    M[2][2] = denom*(nz)
    M[2][3] = denom*(-ax*nx-ay*ny az*nz)

    return M

def mult(M, vec):
    res = [0]*4
    for k in range(4):
        for i in range(4):
            res[k]  = M[k][i] * vec[i]
    return res

#test corners and middle point
M = calcMatrix(1, 0, 0, 0, 1, 0, 0, 0, 1)
#print(M)
p = [1, 0, 0, 1]
print(mult(M, p))
p = [0, 1, 0, 1]
print(mult(M, p))
p = [0, 0, 1, 1]
print(mult(M, p))
p = [1/3, 1/3, 1/3, 1]
print(mult(M, p))

test results:

[0.0, 0.0, 0.0, 1.0]
[1.4142135623730951, 0.0, 0.0, 1.0]
[0.7071067811865476, 1.2247448713915892, 0.0, 1.0]
[0.7071067811865476, 0.4082482904638631, 1.1102230246251565e-16, 1.0]

CodePudding user response：

Find a normal n to the polygon, by means of a cross-product between two non-parallel sides. Take the cross-product of n with a vertical vector, to get an horizontal vector u. Then take the cross product of n and u to get v, and normalize the vectors. u and v are parallel to the plane of the polygon and orthogonal to each other.

Finally, for every vertex p compute the 2D coordinates (p.u, p.v) which show you the polygon in its plane.

numpy supplies the cross and dot vector functions. Also linalg.norm (or sqrt(dot(v, v))).