I have a dataset whereby the outcome variable is split into two groups (patients that had a side-effect or patients that did not). However, it's a bit uneven. (Those that did = 128 and those that did not = 1614). The results are as follows:
Deviance Residuals:
Min 1Q Median 3Q Max
-1.3209 -0.4147 -0.3217 -0.2455 2.7529
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -7.888112 0.859847 -9.174 < 2e-16 ***
age 0.028529 0.009212 3.097 0.00196 **
bmi 0.095759 0.015265 6.273 3.53e-10 ***
surgery_axilla_type11 0.923723 0.524588 1.761 0.07826 .
surgery_axilla_type21 1.607389 0.600113 2.678 0.00740 **
surgery_axilla_type31 1.544822 0.573972 2.691 0.00711 **
cvd1 0.624692 0.290005 2.154 0.03123 *
rt_axilla1 -0.816374 0.353953 -2.306 0.02109 *
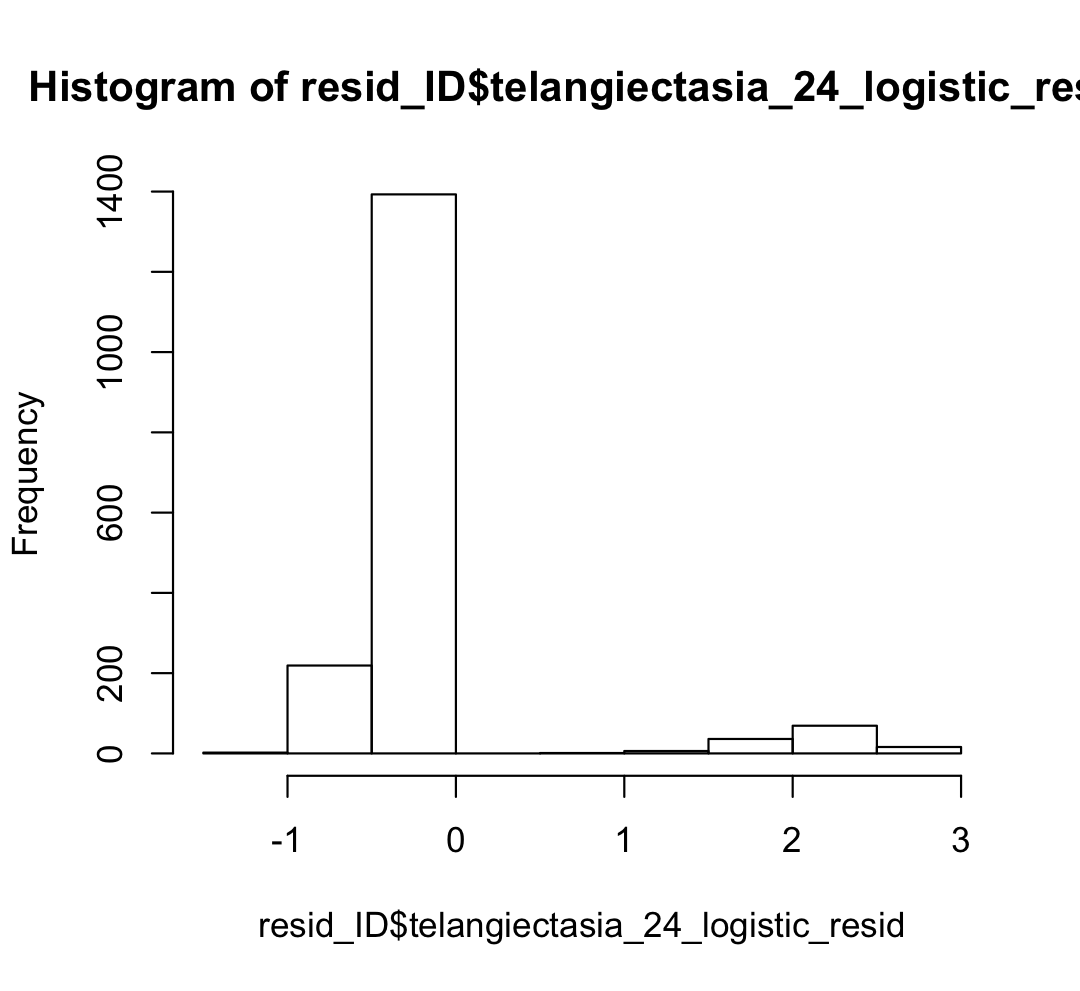
The outcome looks fine and the results seem to make sense, i.e. higher age, bmi, surgery to the armpits, cardiovascular disease increase side effects but when I inspect my residuals - most of them are negative. So I am assuming my model is under-predicting. I am not sure how to conduct any diagnostic plots because for linear regression the plot function in R will check if the residuals look good or if the QQ-plot looks good. I am not really sure how to move beyond checking the results regarding logistic regression. Here is my histogram for the residuals below:
CodePudding user response:
We don't have your data, so let's make a toy example that shows similar results.
Suppose there is a gene with two alleles called "A" and "B". Allele "A" carries a 20% chance of developing a certain disease, and allele "B" carries a 5% chance of developing the same disease. We take a population of 200 people, half of whom have allele "A" and half of whom have allele "B":
set.seed(1)
df <- data.frame(gene = rep(c("A", "B"), each = 100),
disease = c(rbinom(100, 1, 0.2), rbinom(100, 1, 0.05)))
Next, we run a logistic regression to see if there is indeed a difference in the rates of disease between the two alleles:
model <- glm(disease ~ gene, data = df, family = binomial)
summary(model)
#>
#> Call:
#> glm(formula = disease ~ gene, family = binomial, data = df)
#>
#> Deviance Residuals:
#> Min 1Q Median 3Q Max
#> -0.6105 -0.6105 -0.2857 -0.2857 2.5373
#>
#> Coefficients:
#> Estimate Std. Error z value Pr(>|z|)
#> (Intercept) -1.5856 0.2662 -5.956 2.58e-09 ***
#> geneB -1.5924 0.5756 -2.767 0.00566 **
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
#> (Dispersion parameter for binomial family taken to be 1)
#>
#> Null deviance: 134.37 on 199 degrees of freedom
#> Residual deviance: 124.77 on 198 degrees of freedom
#> AIC: 128.77
#>
#> Number of Fisher Scoring iterations: 6
All good so far.
If we predict using the model, we get the expected probability of each person having the disease based on their genotype:
predictions <- predict(model, type = "response")
predictions
#> 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
#> 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17
#> 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36
#> 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17
#> 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54
#> 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17
#> 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72
#> 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17
#> 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90
#> 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17
#> 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108
#> 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04
#> 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126
#> 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04
#> 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144
#> 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04
#> 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162
#> 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04
#> 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180
#> 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04
#> 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198
#> 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04 0.04
#> 199 200
#> 0.04 0.04
Where we see that there is a predicted probability of 0.17 for those with allele "A" having the disease, and a predicted probability of 0.04 for those with allele "B" having the disease.
Note that because the disease has a prevalance of less than 50% in both groups, most predictions will be higher than their actual outcomes (since most outcomes are 0, and all predicted probabilities are greater than zero).
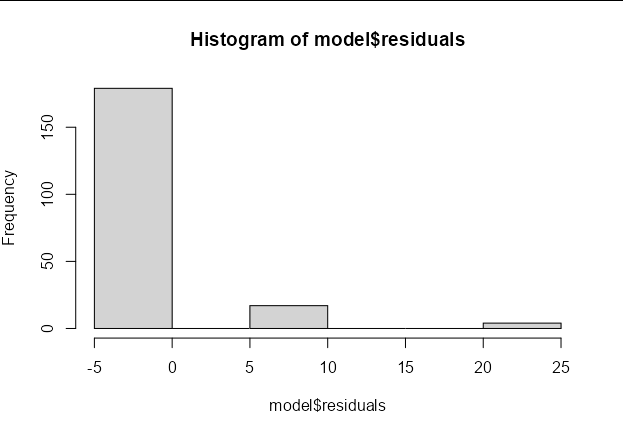
In logistic regression, we are trying to find the probabilities that minimize the squared deviance from each data point to its predicted value. The people who don't have the disease will therefore have negative residuals. So in this example, as in your own data, you will get a large number of small negative residuals, and a small number of large positive residuals (the residuals need to add to zero, after all).
hist(model$residuals)
Note that you would see the opposite pattern of a large number of small positive residuals and a small number of large negative residuals if most of the outcomes were 1 rather than zero.
In short, the distribution of residuals is expected given the distribution of your outcome data.