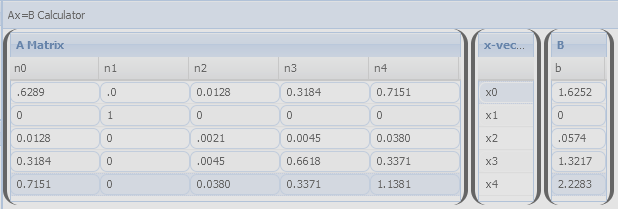
I'm trying to solve linear systems of the form Ax = b where A is an (nxn) matrix of real numbers and b a (1xn) vector of real numbers, using the A = LU algorithm. This is my implementation:

#include <stdio.h>
#include <stdlib.h>
#include <math.h>

int LUPDecompose(double A[N][N], double Tol, int P[N])
{

    int i, j, k, imax;
    double maxA, ptr[N], absA;

    for (i = 0; i <= N; i  )
        P[i] = i; //Unit permutation matrix, P[N] initialized with N

    for (i = 0; i < N; i  ) {
        maxA = 0.0;
        imax = i;

        for (k = i; k < N; k  )
            if ((absA = abs(A[k][i])) > maxA) {
                maxA = absA;
                imax = k;
            }

        if (maxA < Tol) return 0; //failure, matrix is degenerate

        if (imax != i) {
            //pivoting P
            j = P[i];
            P[i] = P[imax];
            P[imax] = j;

            //pivoting rows of A
            for (int ii = 0; ii < N; ii  )
            {
                ptr[ii] = A[i][ii];
                A[i][ii] = A[imax][ii];
                A[imax][ii] = ptr[ii];
            }

            //counting pivots starting from N (for determinant)
            P[N]  ;
        }

        for (j = i   1; j < N; j  ) {
            A[j][i] /= A[i][i];

            for (k = i   1; k < N; k  )
                A[j][k] -= A[j][i] * A[i][k];
        }
    }

    return 1;  //decomposition done
}

/* INPUT: A,P filled in LUPDecompose; b - rhs vector; N - dimension
 * OUTPUT: x - solution vector of A*x=b
 */
void LUPSolve(double A[N][N], int P[N], double b[N], double x[N])
{

    for (int i = 0; i < N; i  ) {
        x[i] = b[P[i]];

        for (int k = 0; k < i; k  )
            x[i] -= A[i][k] * x[k];
    }

    for (int i = N - 1; i >= 0; i--) {
        for (int k = i   1; k < N; k  )
            x[i] -= A[i][k] * x[k];

        x[i] /= A[i][i];
    }
}

int main()
{
    double Am[N][N] = {{0.6289, 0, 0.0128, 0.3184, 0.7151},
                        {0,   1,   0,   0,   0},
                        {0.0128, 0, 0.0021, 0.0045, 0.0380},
                        {0.3184, 0, 0.0045, 0.6618, 0.3371},
                        {0.7151, 0, 0.0380, 0.3371, 1.1381}};
    double bm[N] = {1.6752, 0, 0.0574, 1.3217, 2.2283};
    int Pm[N] = {0};
    double X[N] = {0};

    LUPDecompose( Am, 0.0001, Pm);
    LUPSolve(Am, Pm,  bm, X);

    printf("%f %f %f %f %f",X[0],X[1],X[2],X[3],X[4]);
}

However, I am getting inf values as such.

-1.#IND00 -1.#IND00 3.166387 0.849298 0.670689

I wonder if it is a code issue or algorithm. Any help to solve this issue?

CodePudding user response：

"I wonder if it is a code issue or algorithm. Any help to solve this issue?"

I believe there are code and algorithm issues. The following is your code with corrections to address only compile errors, and warnings (see in-line comments). It is not debugged beyond C syntax to achieve a clean compile, and run w/o error. (i.e. runs with no divide by zero, or inf errors.)

#define N 5 //required to be 5 by hard-coded array definitions in main()

int LUPDecompose(double A[N][N], double Tol, int P[N])
{

    int i, j, k, imax, ii;//added ii here to increase scope below
    double maxA, ptr[N], absA;

    //for (i = 0; i <= N; i  )
    for (i = 0; i < N; i  )
        P[i] = i; //Unit permutation matrix, P[N] initialized with N (actually init with i)

    for (i = 0; i < N; i  ) {
        maxA = 0.0;
        imax = i;

        for (k = i; k < N; k  )
            if ((absA = fabs(A[k][i])) > maxA) {// using fabs, not abs to avoid conversion of double to int.
                maxA = absA;
                imax = k;
            }

        if (maxA < Tol) return 0; //failure, matrix is degenerate

        if (imax != i) {
            //pivoting P
            j = P[i];
            P[i] = P[imax];
            P[imax] = j;

            //pivoting rows of A
           //for (int ii = 0; ii < N; ii  )
           for ( ii = 0; ii < N; ii  )
            {
                ptr[ii] = A[i][ii];
                A[i][ii] = A[imax][ii];
                A[imax][ii] = ptr[ii];
            }

            //counting pivots starting from N (for determinant)
            //P[N]  ;//N will always overflow for array with only N elements
            P[ii-1]  ;//use index here instead
        }

        for (j = i   1; j < N; j  ) {
            A[j][i] /= A[i][i];

            for (k = i   1; k < N; k  ) {//extra brackets added for readability
                A[j][k] -= A[j][i] * A[i][k];
            }
        }
    }

    return 1;  //decomposition done
}

/* INPUT: A,P filled in LUPDecompose; b - rhs vector; N - dimension
 * OUTPUT: x - solution vector of A*x=b
 */
void LUPSolve(double A[N][N], int P[N], double b[N], double x[N])
{

    for (int i = 0; i < N; i  ) {
        x[i] = b[P[i]];
        for (int k = 0; k < i; k  ) {//extra brackets added for readability
            x[i] -= A[i][k] * x[k];
        }
    }

        for (int i = N - 1; i >= 0; i--) {
            for (int k = i   1; k < N; k  ) {//additional brackets added for readability
                x[i] -= A[i][k] * x[k];
            }

            x[i] /= A[i][i];
        }
}
    

//int main()
int main(void)//minimum signature for main includes void
{
    //Note hardcoded arrays in this code require N == 5 (#define at top)
    double Am[N][N] = {{0.6289, 0, 0.0128, 0.3184, 0.7151},
                        {0,   1,   0,   0,   0},
                        {0.0128, 0, 0.0021, 0.0045, 0.0380},
                        {0.3184, 0, 0.0045, 0.6618, 0.3371},
                        {0.7151, 0, 0.0380, 0.3371, 1.1381}};
    double bm[N] = {1.6752, 0, 0.0574, 1.3217, 2.2283};
    int Pm[N] = {0};
    double X[N] = {0};

    LUPDecompose( Am, 0.0001, Pm);
    LUPSolve(Am, Pm,  bm, X);

    printf("%f %f %f %f %f",X[0],X[1],X[2],X[3],X[4]);
    
    return 0;  //int main(void){...} requires return statement.
}  

Based on

the correct solution is:

-0.590174531351002
0
-19.76923076923077
1.0517711171662125
2.6772727272727272

But the actual output from code above is:

Algorithm related debugging is left for you to perform.