I have an (x, y) coordinate (int8_t) and need to rotate them by "x" degrees relative to (0-CodePudding

I'm working in C on a MCU that has no floating points or Math library, and the largest type I have is int32_t.

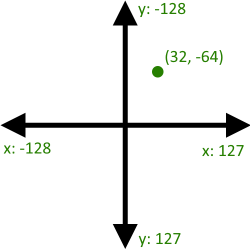
I have an (x, y) coordinate (int8_t) on a graph like this:

A user can say that they want to rotate the location of the point by X degrees (let's say 90°). This is always relative to the center.

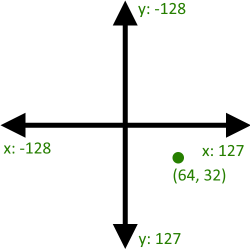
The end result should be (64, 32):

I need to implement this in C with no access to the Math library (no atan2, sin, etc.) The precision I need is in 0.2° increments (so 0.2°, 40.8°, etc. are all valid.)

CodePudding user response：

OP is looking for a full circle non-math.h atan2().

Solve a simpler problem first. Find the arctangent of [0.0 to 1.0] with a "precision I need is in 0.2° increment". The result would be [0.00 ... 45.00] degrees or at least 45/0.2 (225) different values.

In the range 0 to 45 degrees, the arctangent(x) function curves gently. It slope (in radians/x) is near 1.0 when x == 0 to about 0.6187... at x=45 degrees. Is is sufficient to make a uniform lookup table of about 225/0.6187 (364) entries to achieve precision of 0.02 degrees.

Form the look-up table arctan_lu[SCALE_INDEX 1] with pre-calculated values round(radians2degrees(atan(1.0*index/SCALE_INDEX))*100.0) from say, Excel or another C program.

// Number of table lookup entries
#define SCALE_INDEX 364
const int arctan_lu[SCALE_INDEX   1] = { 0, ..., 4500 };  // Values from pre-computation

Then scale the lookup index and lookup the answer.

// Return arc-tangent in centi-degrees [0 ... 4500]
// for an x, y in the first octant:  0 < y < x < INT32_MAX/SCALE_INDEX
// 
int arctagent_primary(int32_t y, int32_t x) {
  int index = SCALE_INDEX*y/x;
  return arctan_lu[index];
}

Now armed with a solution for the first octant, manipulate x,y for the other octants.

// Return arctangent in centi-degrees [0 ... 36000]
// for all x, y
unsigned arctagent_primary(int32_t y, int32_t x) {
  if (y < 0) {
    return 36000 - arctagent_primary(-y, x);
  }
  if (x < 0) {
    return 18000 - arctagent_primary(y, -x);
  }
  if (y >= x) {
    return 9000 - arctagent_primary(x, y);
  }
  if (y > 0) {
    retrun arctagent_primary(y, x);
  }
  return 0; // x,y both 0
}

Additional work needed in arctagent_primary() when x or y are greater than INT32_MAX/SCALE_INDEX. Simply scale them down together.

while (x > INT32_MAX/SCALE_INDEX || y > INT32_MAX/SCALE_INDEX) {
  x /= 2;
  y /= 2;
}

CodePudding user response：

Another option is a pre-computed lookup table for the first quadrant of sin(x).

Since you need 0.2° degrees precision, that would be 450 values in the table. Keep them as int32 fixed-point, with 16 bits fractional part.

If you have that table, you can use 16.16 fixed point math to compute 2x2 rotation matrix, and multiply your point by the matrix.

If you have many points to rotate by the same angle, will probably be faster than the arctangent. Transforming a point with that matrix only takes 4 shifts (two for input, two on output), 4 int32 multiplications, and 2 int32 additions.

P.S. If you really low on memory, use 17.15 fixed point instead of 16.16, this way the lookup table only needs 2 bytes/entry, 900 bytes for the complete table.