I am trying to find a more efficient solution to a combinatorics problem than the solution I have already found.

Suppose I have a set of N objects (indexed 0..N-1) and wish to consider each subset of size K (0<=K<=N). There are S=C(N,K) (i.e., "N choose K") such subsets. I wish to map (or "encode") each such subset to a unique integer in the range 0..S-1.

Using N=7 (i.e., indexes are 0..6) and K=4 (S=35) as an example, the following mapping is the goal:
0 1 2 3 --> 0
0 1 2 4 --> 1
...
2 4 5 6 --> 33
3 4 5 6 --> 34

N and K were chosen small for the purposes of illustration. However, in my actual application, C(N,K) is far too large to obtain these mappings from a lookup table. They must be computed on-the-fly.

In the code that follows, combinations_table is a pre-computed two-dimensional array for fast lookup of C(N,K) values.

All code given is compliant with the C 14 standard.

If the objects in a subset are ordered by increasing order of their indexes, the following code will compute that subset's encoding:

template<typename T, typename T::value_type N1, typename T::value_type K1>
typename T::value_type combination_encoder_t<T, N1, K1>::encode(const T &indexes)
{
   auto offset{combinations_table[N1][K1] - combinations_table[N1 - indexes[0]][K1]};

   for (typename T::value_type index{1}; index < K1;   index)
   {
      auto offset_due_to_current_index{
           combinations_table[N1 - (indexes[index-1]   1)][K1 - index] -
           combinations_table[N1 - indexes[index]][K1 - index]
                                      };

      offset  = offset_due_to_current_index;
   }

   return offset;
}

Here, template parameter T will be either a std::array<> or std::vector<> holding a collection of indexes we wish to find the encoding for.

This is essentially an "order-preserving minimal perfect hash function", as can be read about here:

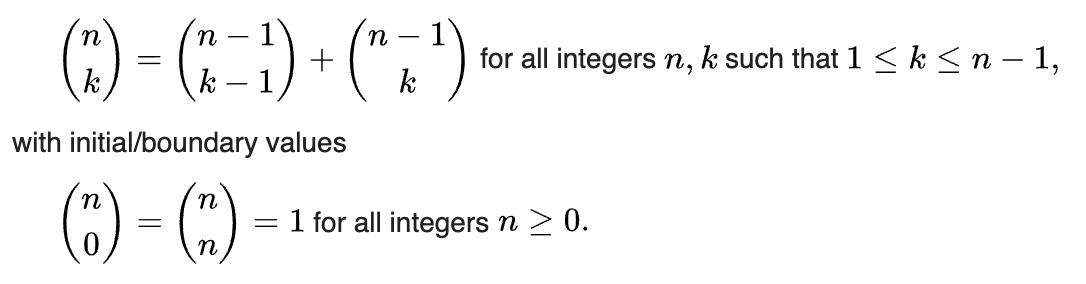
Suppose you have a combination space C(n,k). You can divide that space into two subspaces:

• C(n-1,k-1) all combinations, where the first element of the original set (of length n) is present
• C(n-1, k) where first element is not preset

If you have an index X that corresponds to a combination from C(n,k), you can identify whether the first element of your original set belongs to the subset (which corresponds to X), if you check whether X belongs to either subspace:

• X < C(n-1, k-1) : belongs
• X >= C(n-1, k-1): doesn't belong

Then you can recursively apply the same approach for C(n-1, ...) and so on, until you've found the answer for all n elements of the original set.

Python code to illustrate this approach:

import itertools, math

n=7
k=4
stuff = list(range(n))

# function that maps x into the corresponding combination
def rec(x, n, k, index):
  if n==0 and k == 0:
    return index

  # C(n,k) = C(n-1,k-1)   C(n-1, k)
  # C(n,0) = C(n,n) = 1
  c = math.comb(n-1, k-1) if k > 0 else 0
  if x < c:
    index.add(stuff[len(stuff)-n])
    return rec(x, n-1, k-1, index)
  else:
    return rec(x - c, n-1, k, index)

# Test:
for i,eta in enumerate(itertools.combinations(stuff, k)):
  comb = rec(i, n, k, set())
  print(f'{i} {eta} {comb}')

Produced output:

0 (0, 1, 2, 3) {0, 1, 2, 3}
1 (0, 1, 2, 4) {0, 1, 2, 4}
2 (0, 1, 2, 5) {0, 1, 2, 5}
3 (0, 1, 2, 6) {0, 1, 2, 6}
4 (0, 1, 3, 4) {0, 1, 3, 4}
5 (0, 1, 3, 5) {0, 1, 3, 5}
...
33 (2, 4, 5, 6) {2, 4, 5, 6}
34 (3, 4, 5, 6) {3, 4, 5, 6}

This approach is O(n) (while your approach seems to be O( k * log(n) ) (?) ), and it should have fairly small constant if rewritten iteratively. I'm not sure if it will yield an improvement (needs to be tested).

I also wonder how large your typical k and n values are? I assume they should be small enough so that C(n,k) still fits into 64bits?

Of course, you can use precomputed tables instead of math.comb, replace recursion with iteration (it's tail recursion, so you don't need stack), and use array instead of the set for the result.