Given an unsorted list, say (list a b c ...) where all values are integers. Is there a way to use simple recusion to build a binary search tree.

I'm using the Beginner Student version of Racket.

I know how to solve the problem if the list is sorted, and I know how to solve the problem with an accumulator. I also know I could just sort the list and then use simple recusion. But, without any of these methods, how would I do this?

Example: Given the list (list 1 2 3 5 0 9 3 5 2) the function should produce a binary tree something like

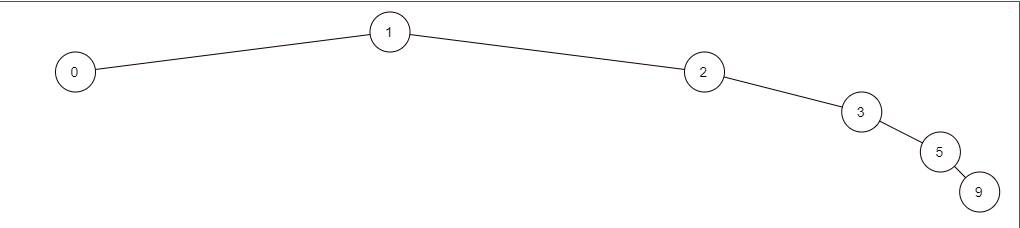
As requested, this is my code for doing the above with an accumulator. I don't have code to perform what I've asked, because I don't know how to make code to do what I've asked.

(define-struct node (key left right))
;; A Node is a (make-node Nat BT BT)

;; A binary tree (BT) is one of:
;;  * empty
;;   * Node

;; (build-bst-from-list list) takes in an unstorted list and builds
;;    a binary search tree using an acculator

;; build-bst-from-list: (listof Num) -> BT
(define (build-bst-from-list list) 
  (build-bst-from-list/acc (rest list) (make-node (first list) empty empty)))

;; (build-bst-from-list/acc list tree) takes in an unstored list and a binary 
;;    tree and inserts all the values from the list into the tree such that
;;    the tree continues to be a binary search tree

;; build-bst-from-list/acc (listof Num) BT -> BT
(define (build-bst-from-list/acc list tree)
  (cond [(empty? list) tree]
        [else (build-bst-from-list/acc (rest list)
                                   (bst-add tree (first list)))]))
;; (bst-add tree value) takes in a binary search tree and a value and
;;    add's the value such that the tree remainder a binary search
;;    tree

;; bst-add: BT Num -> BT
(define (bst-add tree value)
  (cond [(empty? tree) (make-node value empty empty)]
        [(> (node-key tree) value) (make-node (node-key tree)
                                              (bst-add (node-left tree) value)
                                              (node-right tree))]
        [(= (node-key tree) value) tree]
        [else (make-node (node-key tree)
                         (node-left tree)
                         (bst-add (node-right tree) value))]))

CodePudding user response：

Supposing that an empty tree is represented as null and a non-empty tree is represented as (letf root right), you can define a function to insert an item into a binary tree as follows:

(define (insert item tree)
  (cond
    [(empty? tree) (list null item null)]
    [(< item (second tree)) (list (insert item (first tree)) (second tree) (third tree))]
    [(> item (second tree)) (list (first tree) (second tree) (insert item (third tree)))]
    [else tree]))

Then, you can use foldl to create a binary search tree as follows:

(define (create-bst items)
  (foldl insert null items))

Here are some examples:

> (create-bst '(4 6 2 7 1 5 3))
'(((() 1 ()) 2 (() 3 ())) 4 ((() 5 ()) 6 (() 7 ())))

> (create-bst '(1 2 3 5 0 9 3 5 2))
'((() 0 ()) 1 (() 2 (() 3 (() 5 (() 9 ())))))

CodePudding user response：

So, it turns out all I needed to do for this was, well, simple recursion. Simply do the same as I was doing for the accumulator, but instead of inserting into the accumulator, I will insert into the recursive call which creates the rest of the list.

Something like this

(define (bst-from-list list)
  (cond [(empty? list) empty]
        [else (bst-add (bst-from-list (rest list))
                       (first list))]))


(define (bst-add tree value)
  (cond [(empty? tree) (make-node value empty empty)]
        [(> (node-key tree) value) (make-node (node-key tree)
                                              (bst-add (node-left tree) value)
                                              (node-right tree))]
        [(= (node-key tree) value) tree]
        [else (make-node (node-key tree)
                         (node-left tree)
                         (bst-add (node-right tree) value))]))