I found an interesting problem recently, which looks like this:

There is a dull sorting algorithm which takes the 1st number from an array, it finds an element which is lower by 1 than the 1st element (or it takes the highest element when there is no lower one), and puts it in the front. Cost of putting element with index x (counting from 0) in the front is equal to its index. It continues this process until the array is sorted. The task is to count the cost of sorting all the n! permutations of numbers from 1 to n. The answer might be big so the answer should be modulo m (n and m are given in the input)

Example:

Input (n,m): 3 40
Answer: 15

There are permutations of numbers from 1 to 3. The costs of sorting them are:
(1,2,3)->0
(1,3,2)->5
(2,1,3)->1
(2,3,1)->2
(3,1,2)->4
(3,2,1)->3
  sum = 15

My program generates all the possible arrays and sorts them one by one. Its complexity is O(n!*n^2), which is way too high. I am stuck with all my thoughts and this brute force solution.

There are also some funny things I have discovered:

1. When I have grouped the costs of sorting permutations by the quantity of those costs I am getting a strange figure: n=7

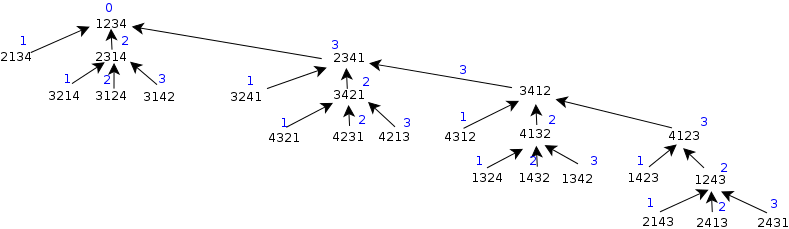
   Now, observe that

   if node==1234 then cost(node) = 0

   if node!=1234 then cost(node) = blue_label(node) cost(parent)

   What you need is to formulate the reverse rule to generate the tree. Maybe use some memoization technique to avoid recomputing cost everytime.