Non-linear regression, nls, in R: singular gradient-CodePudding

I want to fit my data to a specific function that has already been optimized using Matlab.

I get the following error: 'Warning message: Computation failed in stat_smooth(): singular gradient '

Please help! Here is my R code:

tibble
       x     y     SEM
 1     1 0.0342 0.00532
 2     3 0.0502 0.00639
 3     5 0.0700 0.0118 
 4    10 0.123  0.0269 
 5    20 0.154  0.0125 
 6    30 0.203  0.0190 
 7    40 0.257  0.0255 
 8    50 0.287  0.0266 
 9    60 0.345  0.0347 
10    90 0.442  0.0398 
11   120 0.569  0.0570 
12   180 0.726  0.0406 
13   240 0.824  0.0150 
14   360 0.868  0.00821
15  1440 0.890  0.0246 

tibble %>% 
  ggplot(aes(x, y))  
  geom_point() 
  geom_errorbar(aes(ymin=y-SEM, ymax=y SEM), width=25) 
  geom_ribbon(aes(ymin = y-2.575*SEM, ymax = y 2.575*SEM), alpha = 0.1) 
  geom_smooth(method="nls", 
              formula= y ~ (1-((k2/(k2-k1))*exp(-k1*x)) ((k1/(k2-k1))*exp(-k2*x))),
              se=F,
              method.args = list(start=list(k1=0.006999, k2=849.6)))

CodePudding user response：

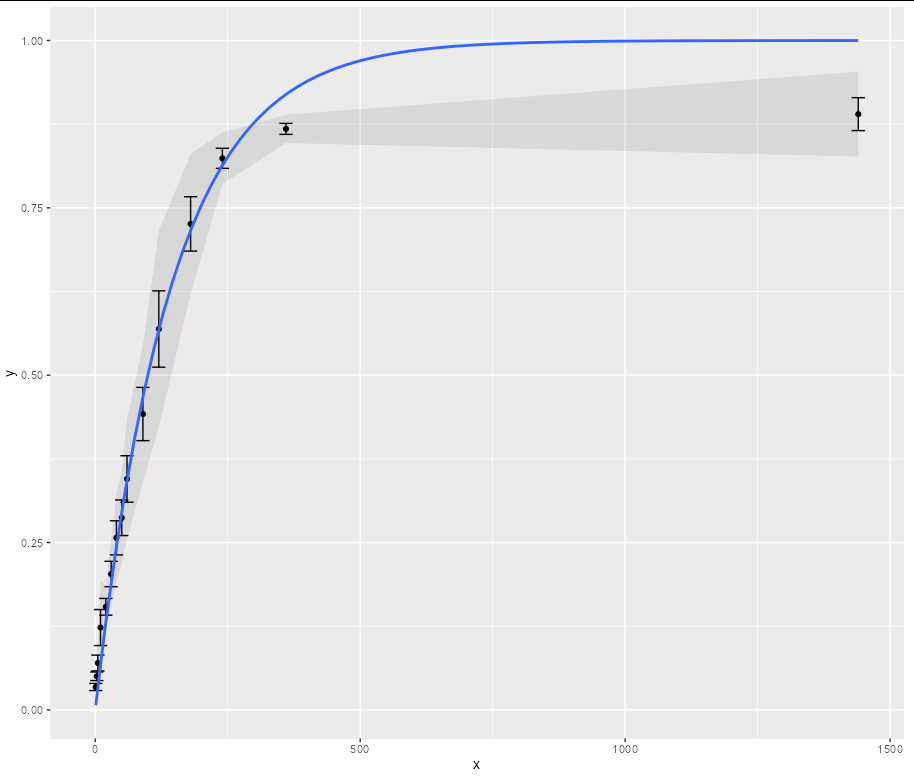
As it stands, nls can't decide on an optimal value of k2 because the sum of squares decreases asymptotically towards a value of about 0.0225 as k2 tends to infinity. There is therefore no finite value of k2 that minimizes the sum of squares. As k2 tends to infinity, it effectively cancels out, to leave the formula equivalent to:

y ~ 1 - exp(-k1*x)

which means that this formula will always fit the data better than the original formula for any finite value of k2.

In short, k2 is a redundant parameter that can only worsen your fit.

Your plot could therefore be made like this:

ggplot(df, aes(x, y))  
  geom_point()  
  geom_errorbar(aes(ymin = y - SEM, ymax = y   SEM), width = 25)  
  geom_ribbon(aes(ymin = y - 2.575 * SEM, ymax = y   2.575 * SEM), alpha = 0.1)  
  geom_smooth(method = "nls", 
              formula = y ~ 1 - exp(-k1 * x),
              se = FALSE,
              method.args = list(start = list(k1 = 0.006999)))

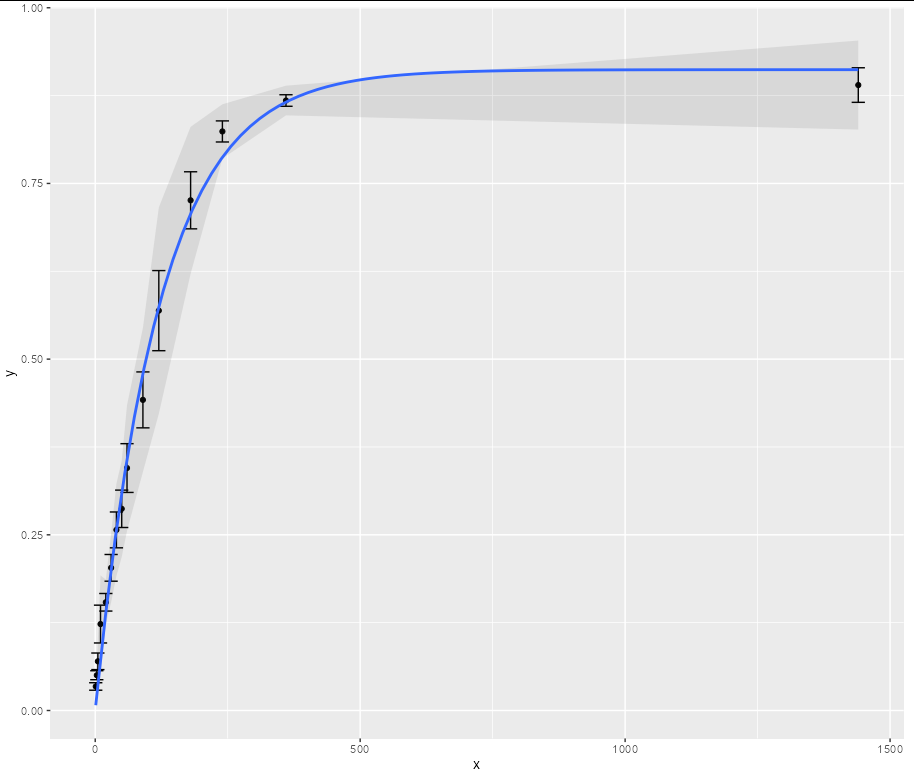
Or, as G. Grothendieck suggests, use an extra parameter to optimize the fit like this (assuming it makes physical sense in your use case)

ggplot(df, aes(x, y))  
  geom_point()  
  geom_errorbar(aes(ymin = y - SEM, ymax = y   SEM), width = 25)  
  geom_ribbon(aes(ymin = y - 2.575 * SEM, ymax = y   2.575 * SEM), alpha = 0.1)  
  geom_smooth(method = "nls", 
              formula = y ~ k2 * (1 - exp(-k1 * x)),
              se = FALSE,
              method.args = list(start = list(k1 = 0.006999, k2 = 1)))