Have been rattling my brain on how best to do this and can not come up a with a good solution. We have a list of thousands of SKUs, that have a few "base" SKUs based on color and then under that variants with different identifiers for example size.
We need to essentially keep one base SKU, remove the other base SKUS, and ensure all the variant SKUs stay under that one base.
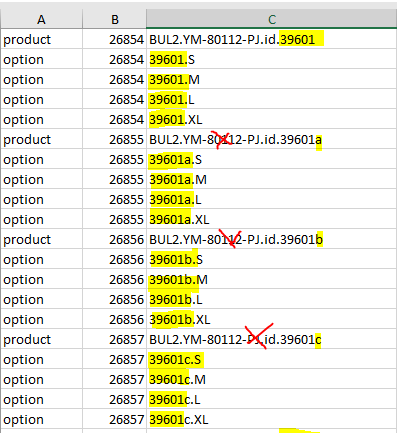
So here is an example, as you see there are essentially 4 base SKUs that are the same but have a sequential letter following the id number after the original first one. BUL2.YM-80112-PJ.id.39601 is the original base SKU, all which then have size sub SKUs.
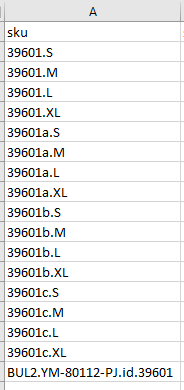
The way we need is shown in picture below where the other base SKUs, the ones with sequential letter are removed and we are left with Original base SKU and all the sub variants. A couple things to note, the number following the "id" will always be 5 numbers, the number of variant sub SKUs vary for example some can have 2 size, some can have six. Also the number of additional base SKUs vary, for example some can just go to "a", others can go to "e"
CodePudding user response:
So you want to
- Keep the entire 39601 series together
- Remove the sku variant lines
- Sort the base SKU to the bottom of the 39601 group.
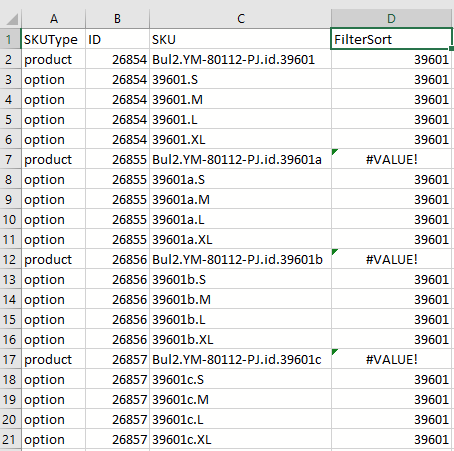
Let's go create a formula in column D that will produce an error for the lines we want to remove, and the SKU group number otherwise.
In column D1 add a column label, I called it FilterSort. In D2, enter the following formula,
=If(A2="option",Value(Left(C2,5)),Value(Right(C2,5)))
This will extract the SKU group number unless it's a Product row and the group ends with a letter where it gives a #Value! error. Fill that formula down to the bottom of your table. You'll see something like this:
Now you can filter out the product lines you don't want by turning on filtering in the Data ribbon, dropping down the FilterSort column, and unselecting the #Value! entry at the list bottom. Then you can sort on column D followed by column A to move the base SKU entry to the bottom, while preserving the internal order of the 39601 rows.