Edit: Seems like my method works.
I encountered a programming question that required me to calculate probability of reaching terminal states.
After a few painstaking hours trying to solve it traditionally, I googled and found that it is called an absorption markov chain. And there is a formula for it.
However, I am trying to figure out what is missing from my solution because it seems correct.
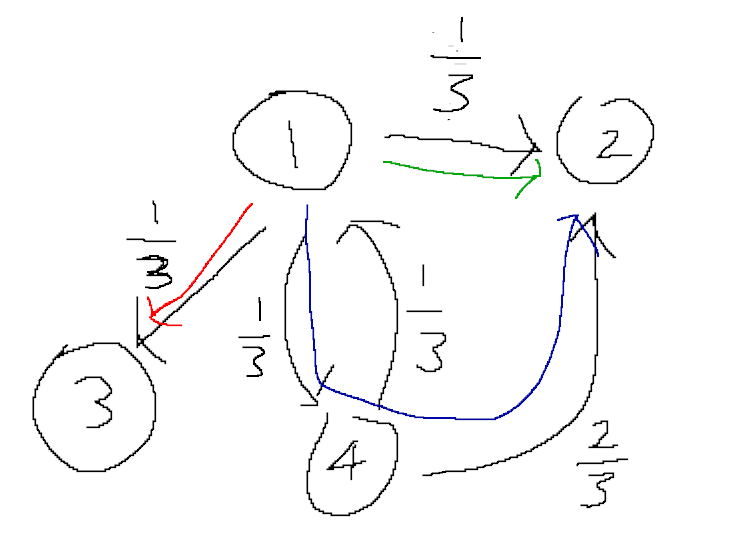
Pardon the crude drawing. Basically there are 4 nodes in this graph, the black lines show the original transitions and probability, while the coloured lines show the paths to termination.
The steps is something like this:
Trace all possible paths to a termination point, sum up the probability of every path to the termination node. That is the probability of reaching the node.
Ignore cyclical paths. Meaning that the "1/3" transition from 4 to 1 is essentially ignored.
Reason for (2): Because we can assume that going back will increase the probability of every possible path in such a way that they still maintain the same relative probability to each other! For example, if I were to go back to 1 from 4, then the chances of going to 2, 3 and 4 will each increase by 1/27 (1/3 * 1/3 * 1/3), making the relative probability still equal to each other!
I hope the above makes sense.
- Calculate the probability of each node as "probability of each node" / "probability of terminating" because by eliminating cyclical graphs, the probability of reaching each node will not be 1 anymore.
So given the above algorithm, here are the values found:
Red path: 1/3
Green path: 1/3
Blue path: 1/3 * 2/3 = 2/9
Probability to reach 3: 1/3
Probability to reach 2: 2/9 1/3 = 5/9
Total probability to terminate: 1/3 5/9 = 8/9
Hence, final probability to reach 3: (1/3) / (8/9) = 3/8
Final probability to reach 2: (5/9) / (8/9) = 5/8
If you are unsure about step (2), we can try it again!
Assume that we went from 1 to 4 and back to 1 again, this has a probability of 1/9.
From here, we can follow each coloured paths again * 1/9 probability.
When combined with the probabilities calculated earlier, this gives us:
10/27 probability to reach 3.
50/81 probability to reach 2.
Total terminating probability of 80/81.
New probability of terminating at 3 is now (10/27) / (80/81) = 3/8 (SAME)
New probability of terminating at 2 is now (50/81) / (80/81) = 5/8 (SAME)
However, the actual probabilities are (2/5) and (3/5) for 3 and 2 respectively, using an algorithm I found online (there is a slim chance it is wrong though).
I realised my answer is actually pretty close, and I am not sure why is it wrong?
CodePudding user response:
We can represent the transitions of the Markov chain with a matrix M. In Python notation, this would look like:
M = [[ 0, 1/3, 1/3, 1/3],
[ 0, 1, 0, 0],
[ 0, 0, 1, 0],
[1/3, 2/3, 0, 0]])
And the probabilities with a vector S, initially with 100% in state 1.
S = [1, 0, 0, 0]
Multiplying S by M gives the new probabilities:
S*M = [0, 1/3, 1/3, 1/3]
S*M**2 = [1/9, 5/9, 1/3, 0]
S*M**3 = [0, 16/27, 10/27, 1/27]
S*M**4 = [1/81, 50/81, 10/27, 0]
S*M**n = [3**(-n)*((-1)**n 1)/2,
3**(-n)*((-1)**n 5*3**n - 6)/8,
3**(-n)*(-(-1)**n 3*3**n - 2)/8,
3**(-n)*(1 - (-1)**n)/2]
In the limit with n going to infinity, for even n, this would give
[0, 5/8, 3/8, 0]
Also starting with 1, 2, 3 and 4 with equal probability:
S = [1/4, 1/4, 1/4, 1/4]
S*M = [1/12, 1/2, 1/3, 1/12]
S*M**2 = [1/36, 7/12, 13/36, 1/36]
S*M**n = [3**(-n)/4, 5/8 - 3*3**(-n)/8, 3/8 - 3**(-n)/8, 3**(-n)/4]
leading to the same limit [0, 5/8, 3/8, 0].
Starting with 1 and 4 with equal probability:
S = [1/2, 0, 0, 1/2]
S*M = [1/6, 1/2, 1/6, 1/6]
S*M**2 = [1/18, 2/3, 2/9, 1/18]
S*M**n = [3**(-n)/2, 3/4 - 3*3**(-n)/4, 1/4 - 3**(-n)/4, 3**(-n)/2]
gives another limit for n going to infinity:
[0, 3/4, 1/4, 0]