Bar chart with positive and negative values-CodePudding

I have the following dataset, in which I want to understand the influence of four explanatory variables (X1, X2, X3 and X4) on the response variable Y:

> dput(data)
structure(list(Y = c("28,1", "27,3", "25,9", "27,2", "30,6", 
"27,6", "28,4", "26,6", "28,1", "30,1", "26,3", "28,4", "26,1", 
"24,6", "26,9", "26,3", "26,7", "26,3", "28,1", "28,2"), X1 = c("27,8", 
"27,7", "26,6", "26,8", "30,7", "27,6", "25,4", "26,7", "26,7", 
"29,4", "25,1", "26,6", "25,2", "24,1", "26,7", "24,9", "26,1", 
"25,5", "27,7", "27,6"), X2 = c("27,5", "27,1", "26,2", "24,8", 
"27,2", "26,3", "23,9", "24,3", "24,1", "25,1", "24", "26,4", 
"24,8", "25,1", "24,2", "25,1", "24,5", "24,1", "25,9", "25,9"
), X3 = c("27,4", "27,4", "26,3", "25,8", "29,2", "27,1", "25", 
"24,8", "25,3", "27,7", "24,9", "25,7", "24,5", "24", "24", "24,4", 
"25,3", "25", "26,8", "27,1"), X4 = c(57L, 54L, 56L, 74L, 62L, 
62L, 67L, 68L, 67L, 63L, 63L, 59L, 70L, 70L, 69L, 67L, 65L, 69L, 
65L, 65L)), class = "data.frame", row.names = c(NA, -20L))

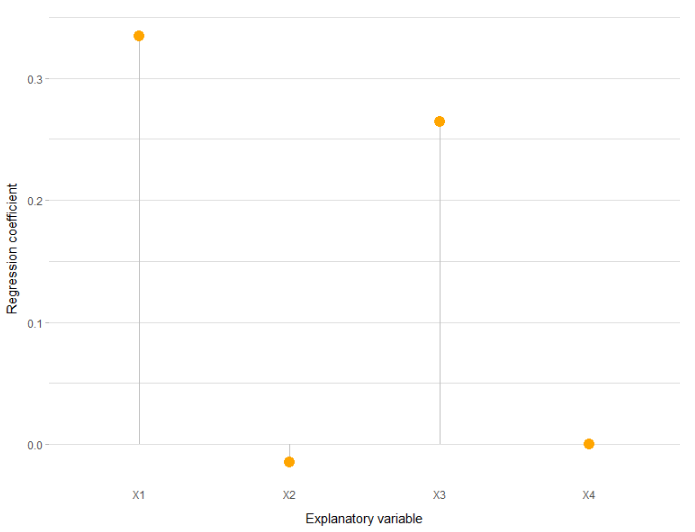
As there is high multicollinearity between the explanatory variables, I decided to use a Ridge Regression. Thus, I created the following lollipop plot to demonstrate the direction (positive or negative) of each variable in the model, from the Ridge regression coefficients:

library(glmnet)
library(ggplot2)
data <- structure(list(Y = c("28,1", "27,3", "25,9", "27,2", "30,6", 
                     "27,6", "28,4", "26,6", "28,1", "30,1", "26,3", "28,4", "26,1", 
                     "24,6", "26,9", "26,3", "26,7", "26,3", "28,1", "28,2"),
               X1 = c("27,8", "27,7", "26,6", "26,8", "30,7", "27,6", "25,4", "26,7", "26,7", 
                      "29,4", "25,1", "26,6", "25,2", "24,1", "26,7", "24,9", "26,1", 
                      "25,5", "27,7", "27,6"),
               X2 = c("27,5", "27,1", "26,2", "24,8", 
                      "27,2", "26,3", "23,9", "24,3", "24,1", "25,1", "24", "26,4", 
                      "24,8", "25,1", "24,2", "25,1", "24,5", "24,1", "25,9", "25,9"),
               X3 = c("27,4", "27,4", "26,3", "25,8", "29,2", "27,1", "25", 
                      "24,8", "25,3", "27,7", "24,9", "25,7", "24,5", "24", "24", "24,4", 
                      "25,3", "25", "26,8", "27,1"),
               X4 = c(57L, 54L, 56L, 74L, 62L, 
                      62L, 67L, 68L, 67L, 63L, 63L, 59L, 70L, 70L, 69L, 67L, 65L, 69L, 
                      65L, 65L)), class = "data.frame", row.names = c(NA, -20L))

#I assume your data is numeric, no strings-columns
data$Y <- as.numeric(gsub(pattern = ",", replacement = ".", data$Y))
data$X1 <- as.numeric(gsub(pattern = ",", replacement = ".", data$X1))
data$X2 <- as.numeric(gsub(pattern = ",", replacement = ".", data$X2))
data$X3 <- as.numeric(gsub(pattern = ",", replacement = ".", data$X3))

#Add a parameter tuning step using cross validation:
fit <- glmnet(x = data[,c("X1", "X2", "X3", "X4")],
              y =  data$Y,
              alpha = 0,
              lambda  = 1)

#Extract data to plot
plot_data <- data.frame(h = names(fit$beta[,1]), v = fit$beta[,1])

#Plot
ggplot(plot_data, aes(x=h, y=v))  
  geom_segment( aes(x=h, xend=h, y=0, yend=v), color="grey")  
  geom_point( color="orange", size=4)  
  theme_light()  
  theme(
    panel.grid.major.x = element_blank(),
    panel.border = element_blank(),
    axis.ticks.x = element_blank(),
    plot.margin = unit(c(0.5,0.5,0.5,0.5), "cm"),
    axis.title.x = element_text(vjust=-2),
    axis.title.y = element_text(angle=90, vjust=3)
  )  
  xlab("Explanatory variable")  
  ylab("Regression coefficient")

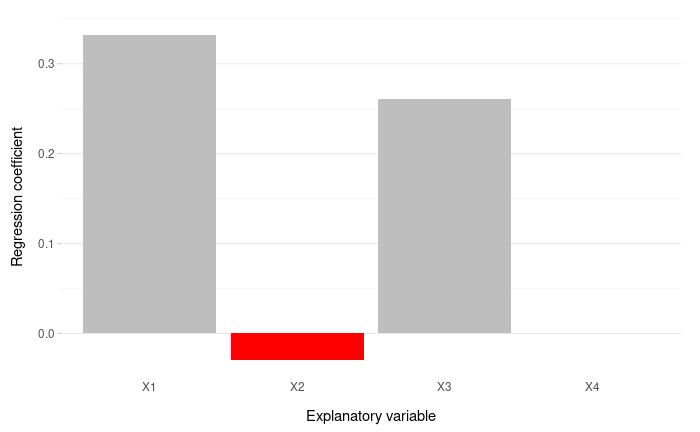
enter image description here

However, how could I make a barplot that presented this same information, being possible to differentiate the positive and negative bars by color? Also, how could I, in barplot, insert negative values on the axis of the graph?

CodePudding user response：

Here's a solution to show your data as barplot and to differentiate between positive (gray) and negative (red) bars by color:

# Extract data to plot
plot_data <- data.frame(h = names(fit$beta[,1]), v = fit$beta[,1]) %>% 
  mutate(fillCol = ifelse(v < 0, "red", "gray"))

# Plot
ggplot(plot_data, aes(x=h, y=v))  
  geom_col(aes(h, v, fill = fillCol))  
  scale_fill_identity()  
  theme_light()  
  theme(
    panel.grid.major.x = element_blank(),
    panel.border = element_blank(),
    axis.ticks.x = element_blank(),
    plot.margin = unit(c(0.5,0.5,0.5,0.5), "cm"),
    axis.title.x = element_text(vjust=-2),
    axis.title.y = element_text(angle=90, vjust=3)
  )  
  xlab("Explanatory variable")  
  ylab("Regression coefficient")