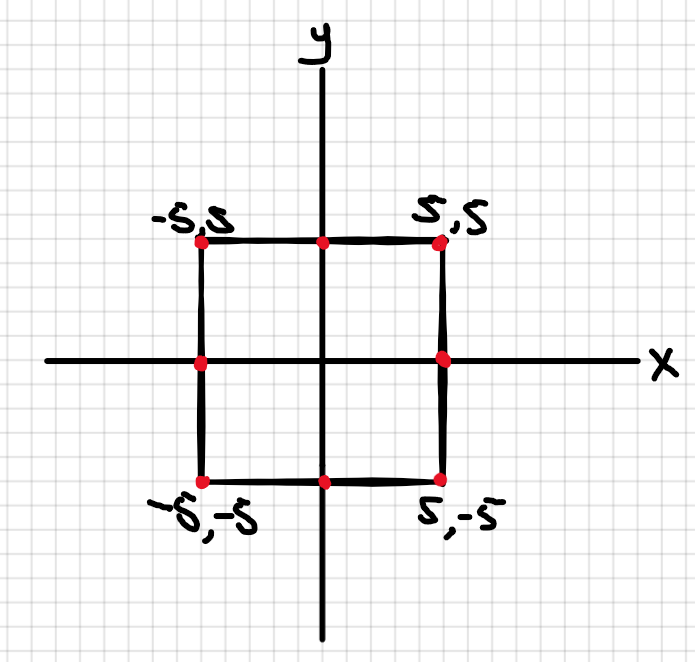
I'm trying to rotate a plane in 3D in Unity, given three points. These points are not always the same, but they are always on the red dots in this image

I know the absolute positions of these points, along with their position relative to the plane. I might for example know that point (-5, 5) is located on (10, -4, 13).

I know that when the three points are on a line (e.g. (-5, 5), (0, 5) and (5, 5)) it's not possible to calculate the complete rotation, so I already throw an exception when this is the case. However, when the three points are not on a single line, it should be possible to calculate the complete rotation.

So far, I've used the code below to rotate, but this misses the rotation around the y-axis (the example uses point (-5, 5), (5, 5) and (-5, -5).

Vector3 p1 = Point1.transform.position;// point 1 absolute position
Vector3 p1Relative = new Vector3(-5, 0, 5);
Vector3 p2 = Point2.transform.position;// point 2 absolute position
Vector3 p2Relative = new Vector3(5, 0, 5);
Vector3 p3 = Point3.transform.position;// point 3 absolute position
Vector3 p3Relative = new Vector3(-5, 0, -5);

Gizmos.DrawSphere(p1, .1f);
Gizmos.DrawSphere(p2, .1f);
Gizmos.DrawSphere(p3, .1f);

Vector3 normal = Vector3.Cross(p2 - p1, p3- p1);
rotator.transform.up = normal;

How would I expand or change this code to include the rotation around the Y-axis? Thank you in advance.

CodePudding user response：

This answer uses this method described by robjohn on math stack exchange.

You can solve for a couple Matrix4x4s that you can use to transform from the first coordinate system to the 2nd, then use that to calculate both the origin (central point) and the rotation to align the axes (using Quaternion.LookRotation);

public class test : MonoBehaviour
{
    [SerializeField] Transform point1;
    [SerializeField] Transform point2;
    [SerializeField] Transform point3;

    [SerializeField] Vector2 relativePos1;
    [SerializeField] Vector2 relativePos2;
    [SerializeField] Vector2 relativePos3;

    [SerializeField] Transform demonstrator;

    void Update()
    {
        Vector3 absolutePos1 = point1.position;
        Vector3 absolutePos2 = point2.position;
        Vector3 absolutePos3 = point3.position;

        Vector3 relativePos4 = (Vector3)relativePos1  
                Vector3.Cross(relativePos2 - relativePos1, 
                relativePos3 - relativePos1);
        Vector3 absolutePos4 = absolutePos1   
                Vector3.Cross(absolutePos2 - absolutePos1, 
                absolutePos3 - absolutePos1);

        Vector4 rightColumn = new Vector4(0, 0, 0, 1);
        Matrix4x4 P = new Matrix4x4(relativePos2 - relativePos1,
                relativePos3 - relativePos1, 
                relativePos4 - (Vector3)relativePos1, rightColumn);
        Matrix4x4 Q = new Matrix4x4(absolutePos2 - absolutePos1, 
                absolutePos3 - absolutePos1, 
                absolutePos4 - absolutePos1, rightColumn);

        Vector3 originPos = TransformPos(P, Q, Vector3.zero);

        // up in source is forward in output        
        Vector3 forwardPos = TransformPos(P, Q, Vector3.up);

        // back in source is up in output
        Vector3 upPos = TransformPos(P, Q, Vector3.back);

        demonstrator.position = originPos;
        demonstrator.rotation = Quaternion.LookRotation(forwardPos 
                - originPos, upPos - originPos);
    }

    Vector3 TransformPos(Matrix4x4 P, Matrix4x4 Q, Vector3 input)
    {
        Matrix4x4 invP = P.inverse;
        return Q * invP * input   ((Vector4)point1.position 
                - Q * invP * relativePos1);
    }
}