From my lecture, I learn that the type of the expression (n `mod` 2 == 0) is Int -> Bool why it is not Int -> Int -> Bool ?

n `mod` 2 has the type (Int -> Int) and if we write n `mod` 2 in the form g = h(n) then (n `mod` 2 == 0) can be write as g(m) which has the type Int -> Bool In the end isn't it shall be the type (Int -> Int -> Bool)?

CodePudding user response：

(n `mod` 2 == 0) has as type Bool, indeed, the expression is equivalent to (==) (mod n 2) 0 and since (==) :: Eq a => a -> a -> Bool returns a Bool if it uses two parameters, this thus means that (n `mod` 2 == 0) has as type Bool. This will require that there is variable named n that is in scope and that n need to have as type n :: Integral a => a, so a value of a type that is a member of the Integral typeclass. It also means that mod n 2 and 0 both have to be of the same type, and that type is a member of the Eq typeclass.

If you construct a function with n as parameter, like \n -> n mod 2 == 0 then it has as type Integral a => a -> Bool, or you can further specialize that to Int -> Bool, since it is a function that maps a parameter n of type Integral a => a or specialized as Int to a Bool.

For the same reason it is not Int -> Int -> Bool: it takes no parameters, and the (n `mod` 2 == 0) itself is an expression that evaluates to a Bool, hence its type is Bool. If you would have constructed a function, like \n -> \m -> n `mod` 2 == 0, its type was Integral a => a -> (b -> Bool) or less verbose Integral a => a -> b -> Bool. Here m can be a value of any type, and its value does not matter for the result of the function. It is thus just an "ad hoc" variable used to make this a function that takes two parameters.

The same holds for n `mod` 2: a more canonical form of this expression is mod n 2, since mod has type mod :: Integral a => a -> a -> a is an expression of type Integral a => a. This type is the same as the type for n and 2. If we make a function with n the parameter, so \n -> n mod 2, then the type of this function is Integral a => a -> a. The type can be specialized to Int -> Int, since Int is a member of the Integral typeclass.

CodePudding user response：

It comes from typing rules. Haskell has bit more rules than given below, but you can start with these.

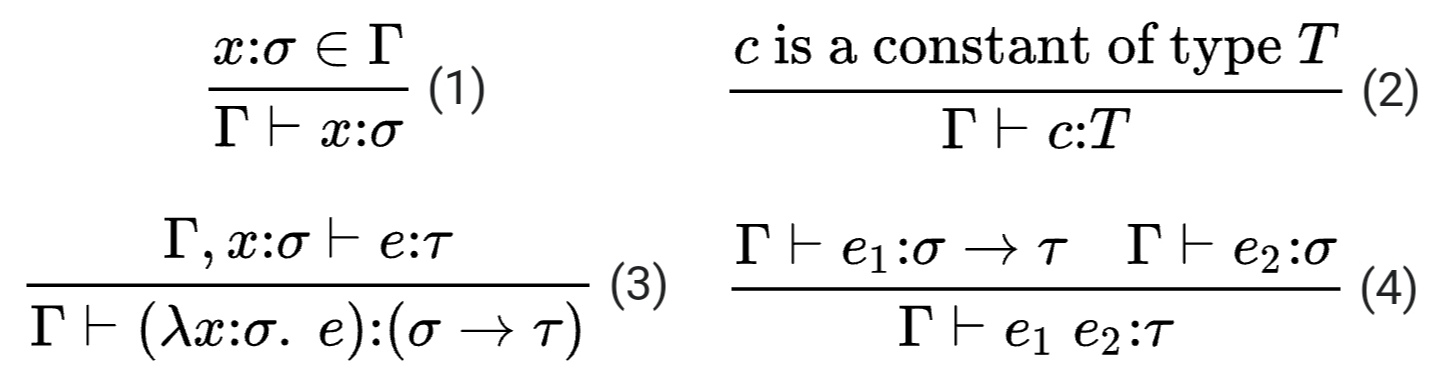
The rule (3) is the only one that constructs a function. Your expression forms from (1,2,4).

If you need further help with these rules, put a comment.