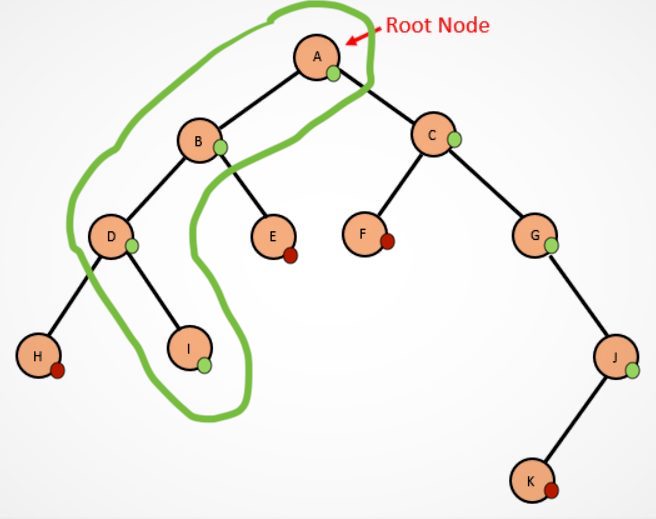
I have a tree (non-binary, unbalanced, no cycles), all nodes have flags (green=active, red=inactive). I'm starting from the root node and I have to find a complete path (from root to leaf) where all nodes are active. (To find at least one path is fine.) As a result, I need the path, not just the info if there is any.

I was thinking of using a depth-first search, but I can't figure out how to include the filtering by active/inactive. Any ideas?

CodePudding user response：

Your DFS recursion will have two base cases:

• A negative one: the current node is not green.
• A positive one: the current node is a green leaf, i.e. it has no children.

In all other cases recursive call(s) have to be made on the node's children. As soon as a positive result comes back from the recursive call, that positive result can be extended with the current node and returned immediately, interrupting the loop.

There are several ways to implement a tree, so I made some choices in this JavaScript implementation:

function findGreenPath(tree, label) {
    let root = tree[label];
    if (!root.green) return null; // No path through none-green node
    if (root.children == "") return label; // It is a leaf, start a path
    for (let child of root.children) {
        let path = findGreenPath(tree, child);
        if (path != null) return label   path; // prepend this node to a good path
    }
    return null; // No path found
}

// Implementation of the example tree in the question:
let tree = { // Dictionary of nodes by their label
    "A": {green: true, children: "BC"},
    "B": {green: true, children: "DE"},
    "C": {green: true, children: "FG"},
    "D": {green: true, children: "HI"},
    "E": {green: false, children: ""},
    "F": {green: false, children: ""},
    "G": {green: true, children: "J"},
    "H": {green: false, children: ""},
    "I": {green: true, children: ""},
    "J": {green: true, children: "K"},
    "K": {green: false, children: ""}
};

let path = findGreenPath(tree, "A"); 

console.log(path); // ABDI

<iframe name="sif1" sandbox="allow-forms allow-modals allow-scripts" frameborder="0"></iframe>

CodePudding user response：

It's straightforward. As you know, DFS can be implemented by a stack. Such that we push the root of the tree into the stack, and afterward pop the top of the stack and push children of the popped node. We continue this process up to have an empty stack.

Now, for your case, just before pushing the nodes into the stack, you need to check whether the specified node (i.e., children of the popped node) is active or inactive. In that case, you will not search down when reaching an inactive node. Finally, only report all generated paths that their end node is a leaf (you can easily find the leaves during the search, a node that does not have any child).