We are given a graph of N nodes. (1-N), where each node has exactly 1 directed edge to some node (this node can be the same node).
We need to answer the queries of type : A, B, which asks time required when 2 objects collide if one start at A and other start at B. Both moves 1 hop in 1 sec. If it's not possible for them to collide time would be -1.
Time : from X -> to Y : 1 hop = 1 second.
Constraints :
N, Q <= 10^5 (number of nodes, number of queries).
Example : for given graph
A -> B -> C -> D -> E
^ |
K <- F
Query(A, E) : 3 seconds, as at time t = 3 secs they both will be on node D.
Query(C, D) : -1 seconds, as they will never collide.
What's the optimal way to answer each query?
Brute Force Approach: time - O(Q * N)
Improved solution using binary lifting technique: time - O(Q * log(N))
private static int[] collisionTime(int N, int Q, int[] A, int[][] queries) {
// ancestor matrix : creation time- O(n * log(n))
int M = (int) (Math.ceil(Math.log10(N) / Math.log10(2))) 1;
int[][] ancestor = new int[N 1][M];
for(int i = 1; i <= N; i ) {
ancestor[i][0] = A[i]; // 2^0-th ancestor.
}
for(int j = 1; j < M; j ) {
for(int i = 1; i <= N; i ) {
ancestor[i][j] = ancestor[ancestor[i][j-1]][j-1];
}
}
int[] answer = new int[Q];
for(int i = 0; i < Q; i ) {
int u = queries[i][0];
int v = queries[i][1];
answer[i] = timeToCollide(u, v, ancestor);
}
return answer;
}
// using binary lifting: time- O(log(n))
private static int timeToCollide(int u, int v, int[][] ancestor) {
int m = ancestor[0].length;
// edge cases
if(u == v) // already in collision state
return 0;
if(ancestor[u][m-1] != ancestor[v][m-1]) // their top most ancestor is not the same means they cannot collide at all.
return -1;
int t = 0;
for(int j = m - 1; j >=0; j--) {
if(ancestor[u][j] != ancestor[v][j]) {
u = ancestor[u][j];
v = ancestor[v][j];
t = Math.pow(2, j);
}
}
return t 1;
}
CodePudding user response:
It is only possible for a collision to occur on a node that has more than 1 link leading to it. Node D in your example.
Let's call these nodes "crash sites"
So you can prune your graph down to just the crash site nodes. The nodes that lead to the crash site nodes become attributes of the crash site nodes.
Like this for your example:
D : { A,B,C }, { E,F,K }
A collision can ONLY occur if the starting nodes are on two different attribute lists of the same crash site node.
Once you are sure a crash can occurr, then you can check that both starting nodes are the same distance from the crash site.
Algorithm:
Prune graph to crash site nodes
LOOP over questions
Get 2 start nodes
LOOP over crash sites
IF start nodes on two different attributes of crash site
IF start nodes are equi-distant from crash site
report crash time
BREAK from crash site loop
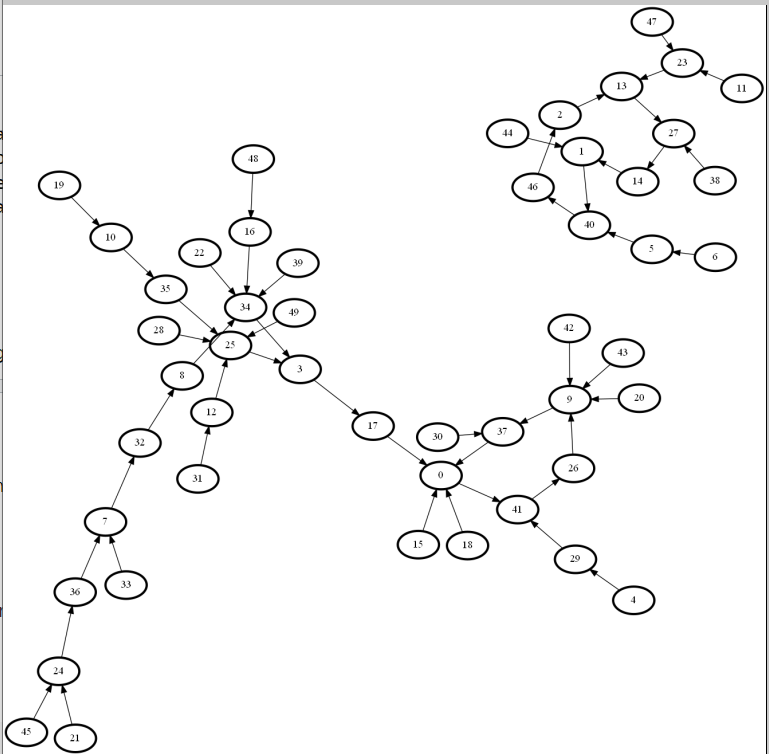
Here is a randomly generated graph with 50 nodes where every node has one out edge connected to another node chosen randomly
The collision sites are
5 7 8 9 10 11 18 19 23 25 31 33 36 37 39
So the algorithm need only loop over 15 nodes, at most, instead of 50.
The answer to the question 'do two particular nodes collide?' is almost always 'NO'. It is kind of boring that way. So let's ask a slightly different question: 'for a particular graph, which pairs of nodes result in a collision?' This requires the same algorithm ( applied to every pair of nodes ) but alway produces an interesting answer.
for this graph
I get this answer
0 and 29 collide at 41
1 and 5 collide at 40
2 and 23 collide at 13
8 and 16 collide at 34
8 and 22 collide at 34
8 and 39 collide at 34
9 and 30 collide at 37
10 and 31 collide at 25
11 and 47 collide at 23
12 and 28 collide at 25
12 and 35 collide at 25
12 and 49 collide at 25
13 and 38 collide at 27
14 and 44 collide at 1
15 and 17 collide at 0
15 and 18 collide at 0
15 and 37 collide at 0
16 and 22 collide at 34
16 and 39 collide at 34
17 and 18 collide at 0
17 and 37 collide at 0
18 and 37 collide at 0
20 and 26 collide at 9
20 and 42 collide at 9
20 and 43 collide at 9
21 and 45 collide at 24
22 and 39 collide at 34
25 and 34 collide at 3
26 and 42 collide at 9
26 and 43 collide at 9
28 and 35 collide at 25
28 and 49 collide at 25
32 and 48 collide at 34
33 and 36 collide at 7
35 and 49 collide at 25
42 and 43 collide at 9
Some timing results
| Node Count | Crash Sites millisecs |
Question Count | Question mean microsecs |
|---|---|---|---|
| 50 | 0.4 | 1225 | 0.02 |
| 500 | 50 | 124750 | 0.02 |
| 5000 | 5500 | ~12M | 0.02 |
| 10000 | 30000 | ~50M | 0.03 |
| 30000 | 181000 | ~450M | 0.6 |
Notes:
- The mean time for a question is the average of checking every possible pair of nodes for a possible collision.
- Answering a single question is extremely fast, about 20 nanoseconds for moderately sized graphs ( < 10,000 nodes ) [ A previous timing report included outputting the results when a collision was found, which takes much longer than detecting the collision. These results were taken with all output to the console commented out. ]
- Setting up the crash sites and their tributaries gets slow with moderately sized graphs ( > 5,000 nodes ). It is only worth doing if a lot of questions are going to be asked.
The code for this is available at https://github.com/JamesBremner/PathFinder
CodePudding user response:
- Find all the terminal cycles and designate an arbitrary vertex in each terminal cycle as the cycle root (O(N))
- For each vertex, record the length of its terminal cycle, its distance to entry into the terminal cycle, and the distance to the terminal cycle root (O(N)).
- Sever the outgoing link from each cycle root. This turns the graph into a forest.
- For each query, find the closest (lowest) common ancestor of the two query nodes in this forest.
- From the information saved about each query node and the lowest common ancestor, you can figure out the time to collision in constant time.
Step (4), the lowest common ancestor query, is a very well-studied problem. The best algorithms require only linear processing time and provide constant query time, leading to O(N Q) time for this problem all together.