I am trying to apply the idea of sklearn

Kind of straight line bending once. I would like to see the model performance at different thresholds, not just one, a figure similar to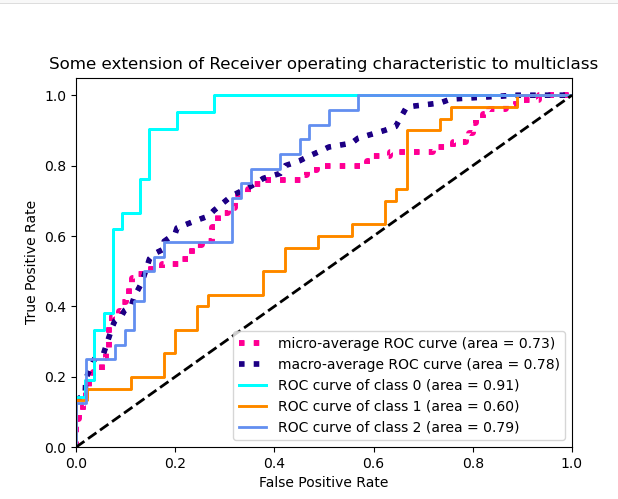

CodePudding user response：

• Point is that you're using predict() rather than predict_proba()/decision_function() to define your y_hat. This means - considering that the threshold vector is defined by the number of distinct values in y_hat (see here for reference), that you'll have few thresholds per class only on which tpr and fpr are computed (which in turn implies that your curves are evaluated at few points only).

• Indeed, consider what the doc says to pass to y_scores in roc_curve(), either prob estimates or decision values. In the example from sklearn, decision values are used to compute the scores. Given that you're considering a RandomForestClassifier(), considering probability estimates in your y_hat should be the way to go.

• What's the point then of label-binarizing the output? The standard definition for ROC is in terms of binary classification. To pass to a multiclass problem, you have to convert your problem into binary by using OneVsAll approach, so that you'll have n_class number of ROC curves. (Observe, indeed, that as SVC() handles multiclass problems in a OvO fashion by default, in the example they had to force to use OvA by applying OneVsRestClassifier constructor; with a RandomForestClassifier you don't have such problem as that's inherently multiclass, see here for reference). In these terms, once you switch to predict_proba() you'll see there's no much sense in label binarizing predictions.

   # all imports
   import numpy as np
   import matplotlib.pyplot as plt
   from itertools import cycle
   from sklearn import svm, datasets
   from sklearn.metrics import roc_curve, auc
   from sklearn.model_selection import train_test_split
   from sklearn.preprocessing import label_binarize
   from sklearn.datasets import  make_classification
   from sklearn.ensemble import RandomForestClassifier
   # dummy dataset
   X, y = make_classification(10000, n_classes=5, n_informative=10, weights=[.04, .4, .12, .5, .04])
   train, test, ytrain, ytest = train_test_split(X, y, test_size=.3, random_state=42)
  
   # random forest model
   model = RandomForestClassifier()
   model.fit(train, ytrain)
   yhat = model.predict_proba(test)
  
   def plot_roc_curve(y_test, y_pred):
       n_classes = len(np.unique(y_test))
       y_test = label_binarize(y_test, classes=np.arange(n_classes))
  
       # Compute ROC curve and ROC area for each class
       fpr = dict()
       tpr = dict()
       roc_auc = dict()
       thresholds = dict()
       for i in range(n_classes):
         fpr[i], tpr[i], thresholds[i] = roc_curve(y_test[:, i], y_pred[:, i], drop_intermediate=False)
       roc_auc[i] = auc(fpr[i], tpr[i])
  
       # Compute micro-average ROC curve and ROC area
       fpr["micro"], tpr["micro"], _ = roc_curve(y_test.ravel(), y_pred.ravel())
       roc_auc["micro"] = auc(fpr["micro"], tpr["micro"])
  
       # First aggregate all false positive rates
       all_fpr = np.unique(np.concatenate([fpr[i] for i in range(n_classes)]))
  
       # Then interpolate all ROC curves at this points
       mean_tpr = np.zeros_like(all_fpr)
       for i in range(n_classes):
         mean_tpr  = np.interp(all_fpr, fpr[i], tpr[i])
  
       # Finally average it and compute AUC
       mean_tpr /= n_classes
  
       fpr["macro"] = all_fpr
       tpr["macro"] = mean_tpr
       roc_auc["macro"] = auc(fpr["macro"], tpr["macro"])
  
       # Plot all ROC curves
       #plt.figure(figsize=(10,5))
       plt.figure(dpi=600)
       lw = 2
       plt.plot(fpr["micro"], tpr["micro"],
       label="micro-average ROC curve (area = {0:0.2f})".format(roc_auc["micro"]),
       color="deeppink", linestyle=":", linewidth=4,)
  
       plt.plot(fpr["macro"], tpr["macro"],
       label="macro-average ROC curve (area = {0:0.2f})".format(roc_auc["macro"]),
       color="navy", linestyle=":", linewidth=4,)
  
       colors = cycle(["aqua", "darkorange", "darkgreen", "yellow", "blue"])
       for i, color in zip(range(n_classes), colors):
         plt.plot(fpr[i], tpr[i], color=color, lw=lw,
         label="ROC curve of class {0} (area = {1:0.2f})".format(i, roc_auc[i]),)
  
       plt.plot([0, 1], [0, 1], "k--", lw=lw)
       plt.xlim([0.0, 1.0])
       plt.ylim([0.0, 1.05])
       plt.xlabel("False Positive Rate")
       plt.ylabel("True Positive Rate")
       plt.title("Receiver Operating Characteristic (ROC) curve")
       plt.legend()
  

Eventually, consider that roc_curve() has also a drop_intermediate parameter meant for dropping suboptimal thresholds (it might be useful to know).