Group by float values by range-CodePudding

Let's say I have a data frame that looks like that:

Result
0.001
0.000
-0.001
0.005
0.002
0.003
0.004
0.001
3.400
3.401
3.405
3.402
0.003
0.004
0.001
4.670
-0.001
4.675
4.672
0.003
3.404

I would like to group values by some interval (let's say ±0.005 from first 'not already existing' value), so here I would have it grouped as:

Result GROUP_AVG
0.001  0.003
0.000  0.003
-0.001  0.003
0.005  0.003
0.002  0.003
0.003  0.003
0.004  0.003
0.001  0.003
3.400  3.403
3.401  3.403
3.405  3.403
3.402  3.403
0.003  0.003
0.004  0.003
0.001  0.003
4.670  4.673
-0.001  0.003
4.675  4.673
4.672  4.673
0.003  0.003
3.404  3.403

Now, I am doing it inefficient way:

Check if row_value is in ±0.005 from any item from averages_set["value"]
If no, create new entity in averages_set with "value": row_value, "average": row_value, count: 1
If yes, update averages_set[i]["average"]=(average * count row_value)/(count 1), and also count=count 1
After all the rows are iterated, add column to basic dataset and change it for each row based on its distance to averages_set[i]["value"], change the new column value for row with averages_set[i]["average"] as I need to have average anyway for further operations. And the average can be actually treated as discrete value without bigger problems for further operations.

I have used pandas.groupby before, and it works great for discrete values. Is there a way to, for example, group by based on float value, taking into account e.g. ±0.5 from the first new value that occurred? It was much more efficient than my algorithm, and I could easily calculate average(and not only) for each group.

CodePudding user response：

Your problem is difficult to solve optimally (i.e., find the minimum number of groups). As noted in the comments, your approach is order-dependent: [0, 0.006, 0.004] would yield two groups ([0, 0.005]) whereas [0, 0.004, 0.006] would yield a single one ([0.0033..]). Furthermore, it is a greedy agglomerative grouping, which cuts many of the possible groups, often including the optimal one.

Here is one approach using agglomerative clustering. It is between O(n log n) and O(n^2) for n points: roughly 61ms for 1K points, but 3.2s for 5K points on my machine. It also requires a slight change of definition: we represent groups by a "center" (the center of the bounding box) rather than an average centroid.

We use the linkage='complete' linkage type (so the overall diameter of the cluster is the determining metric) and set the maximum distance (that diameter) to be twice your "tolerance".

Example

from sklearn.cluster import AgglomerativeClustering

def quantize(df, tolerance=0.005):
    # df: DataFrame with only the column(s) to quantize
    model = AgglomerativeClustering(distance_threshold=2 * tolerance, linkage='complete',
                                    n_clusters=None).fit(df)
    df = df.assign(
        group=model.labels_,
        center=df.groupby(model.labels_).transform(lambda v: (v.max()   v.min()) / 2),
    )
    return df

On your data, it takes 4.4ms and results in the following df:

>>> quantize(df[['Result']], tolerance=0.005)
    Result  group  center
0    0.001      0  0.0020
1    0.000      0  0.0020
2   -0.001      0  0.0020
3    0.005      0  0.0020
4    0.002      0  0.0020
5    0.003      0  0.0020
6    0.004      0  0.0020
7    0.001      0  0.0020
8    3.400      2  3.4025
9    3.401      2  3.4025
10   3.405      2  3.4025
11   3.402      2  3.4025
12   0.003      0  0.0020
13   0.004      0  0.0020
14   0.001      0  0.0020
15   4.670      1  4.6725
16  -0.001      0  0.0020
17   4.675      1  4.6725
18   4.672      1  4.6725
19   0.003      0  0.0020
20   3.404      2  3.4025

Visualization

You can visualize the corresponding dendrogram with scipy.cluster.hierarchy.dendrogram:

from scipy.cluster.hierarchy import dendrogram, linkage
from scipy.spatial.distance import pdist

Z = linkage(pdist(df[['Result']]), 'complete')
dn = dendrogram(Z)
plt.axhline(2 * tolerance, c='k')
plt.ylim(0, 2.1 * tolerance)

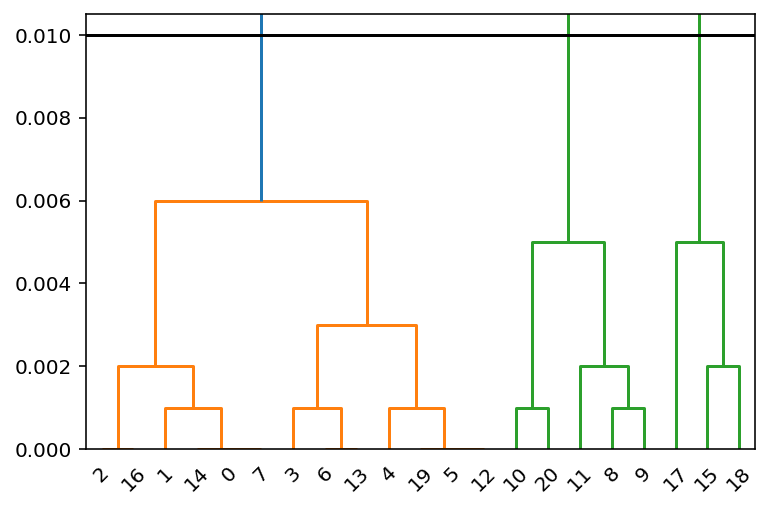
There are three clusters below the threshold indicated by 2 * tolerance.

Speed

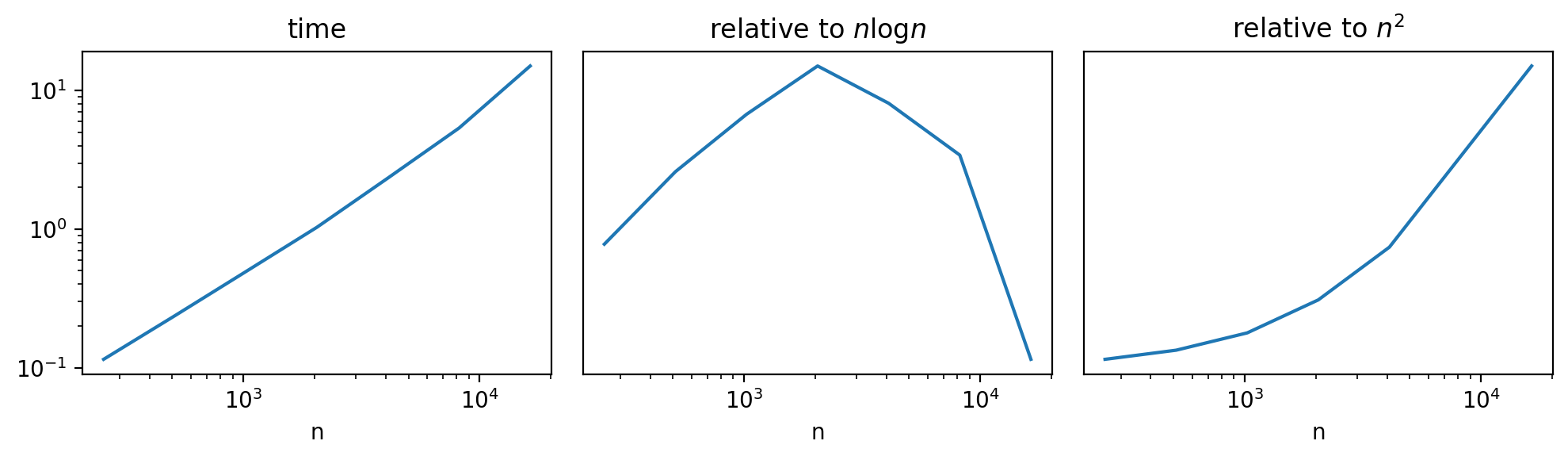
The hierarchical clustering with linkage='complete' is generally O(n^2). In some cases though, there might be a bit of saving because of the distance_threshold. To see the effect of this, we use perfplot and explore performance v. size of df:

import perfplot

tolerance = 0.005
base2_max = int(np.round(np.log2(20_000)))
o = perfplot.bench(
    setup=lambda n: pd.DataFrame(np.random.uniform(0, tolerance * n, size=n), columns=['Result']),
    kernels=[quantize],
    n_range=[2 ** k for k in range(8, base2_max   1)],
)

The time is above n log(n), but clearly not quite n^2:

k_ = o.n_range
t_ = o.timings_s[0]

fig, axes = plt.subplots(ncols=3, figsize=(10, 3), tight_layout=True)
axes = iter(axes)
ax = next(axes)
ax.loglog(k_, t_)
ax.set_title('time')
ax.set_xlabel('n')

ax = next(axes)
ax.semilogx(k_, np.log(k_) * k_ / t_)
ax.set_title('relative to $n \log n$')
ax.set_xlabel('n')
ax.axes.get_yaxis().set_visible(False)

ax = next(axes)
ax.semilogx(k_, k_ ** 2 / t_)
ax.set_title('relative to $n^2$')
ax.set_xlabel('n')
ax.axes.get_yaxis().set_visible(False)