How to use a for loop over negative (and positive) values in R?-CodePudding

I am trying to use a for-loop over a range of positive and negative values and then plot the results. However, I'm having trouble getting R not to plot the correct values, since the negative values seem to screw up the index.

More precisely, the code I am running is:

# Setup objects
R = (1:20)
rejection = rep(NA, 20)
t = seq(from = -10, to = 10, by = 1)
avg_rej_freq = rep(NA, 21)

# Test a hypothesis for each possible value of x and each replication
for (x in t) {
  for (r in R) {
    # Generate 1 observation from N(x,1)
    y =  rnorm(1, x, 1)
    # Take the average of this observation
    avg_y = mean(y)
    # Test this observation using the test we found in part a
    if (avg_y >= 1   pnorm(.95))
    {rejection[r] = 1}
    if (y < 1   pnorm(.95))
    {rejection[r] = 0}
  }
  # Calculate the average rejection frequency across the 20 samples
  avg_rej_freq[x] = mean(rejection)
}

# Plot the different values of x against the average rejection frequency
plot(t, avg_rej_freq)

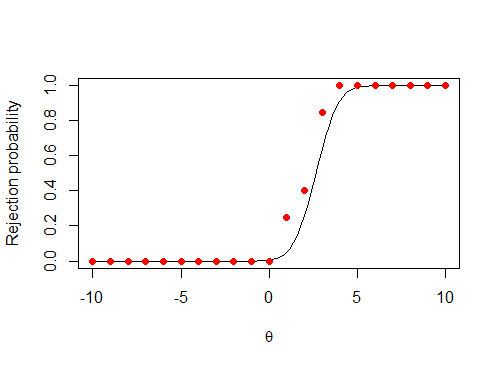
The resulting graph should look something like this

# Define the rejection probability for n=1
rej_prob = function(x)(1-pnorm(1-x qnorm(0.95)))

# Plot it
curve(rej_prob,from = -10, to = 10, xlab = expression(theta), 
      ylab = "Rejection probability")

...but there's clearly something wrong with my code that is shifting the positive values on the graph over to the left.

Any help on how to fix this would be much appreciated!

CodePudding user response：

Yep, as you suspected the negative indices are causing problems. R doesn't know how to store something as the "negative first" object in a vector, so it just drops them. Instead, try using seq_along to produce a vector of all positive indices and looping over those instead:

# Setup objects
R = (1:20)
rejection = rep(NA, 20)
t = seq(from = -10, to = 10, by = 1)
avg_rej_freq = rep(NA, 21)

# Test a hypothesis for each possible value of x and each replication
for (x in seq_along(t)) {
  for (r in R) {
    # Generate 1 observation from N(x,1)
    # Now we ask for the value of t at index x rather than t directly
    y =  rnorm(1, t[x], 1)
    # Take the average of this observation
    avg_y = mean(y)
    # Test this observation using the test we found in part a
    if (avg_y >= 1   pnorm(.95))
    {rejection[r] = 1}
    if (y < 1   pnorm(.95))
    {rejection[r] = 0}
  }
  # Calculate the average rejection frequency across the 20 samples
  avg_rej_freq[x] = mean(rejection)
}

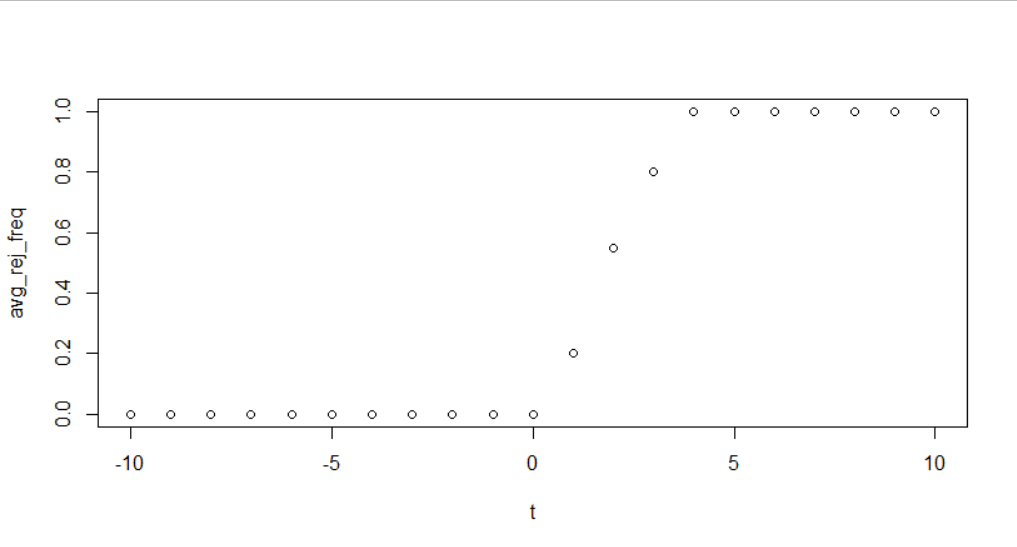
# Plot the different values of x against the average rejection frequency
plot(t, avg_rej_freq)

which produces the following plot:

CodePudding user response：

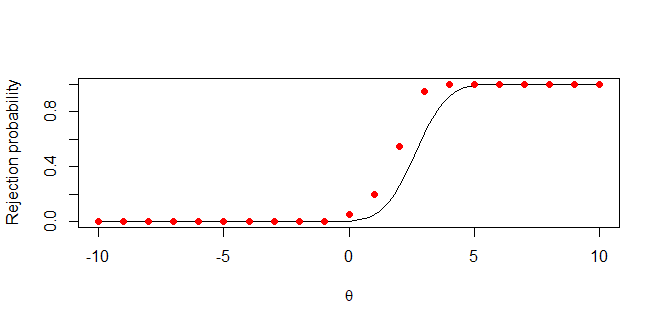
Not sure why you want to simulate the vectorized function pnrom() using for loops, still correcting the mistakes in your code (check the comments):

# Test a hypothesis for each possible value of x and each replication
for (x in t) {
  for (r in R) {
    # Generate 1 observation from N(x,1)
    y =  rnorm(1, x, 1)
    # no need to take average since you have a single observation
    # Test this observation using the test we found in part a
    rejection[r] = ifelse(y >= 1   pnorm(.95), 1, 0)
  }
  # Calculate the average rejection frequency across the 20 samples
  # `R` vector index starts from 1, transform your x values s.t., negative values become positive
  avg_rej_freq[x-min(t) 1] = mean(rejection)
}


# Define the rejection probability for n=1
rej_prob = function(x)(1-pnorm(1-x qnorm(0.95)))

# Plot it
curve(rej_prob,from = -10, to = 10, xlab = expression(theta), 
      ylab = "Rejection probability")

# plot your points
points(t, avg_rej_freq, pch=19, col='red')

CodePudding user response：

Not sure why the for loops etc, what you are doing can be collapsed into a one line. The rest of the code taken from