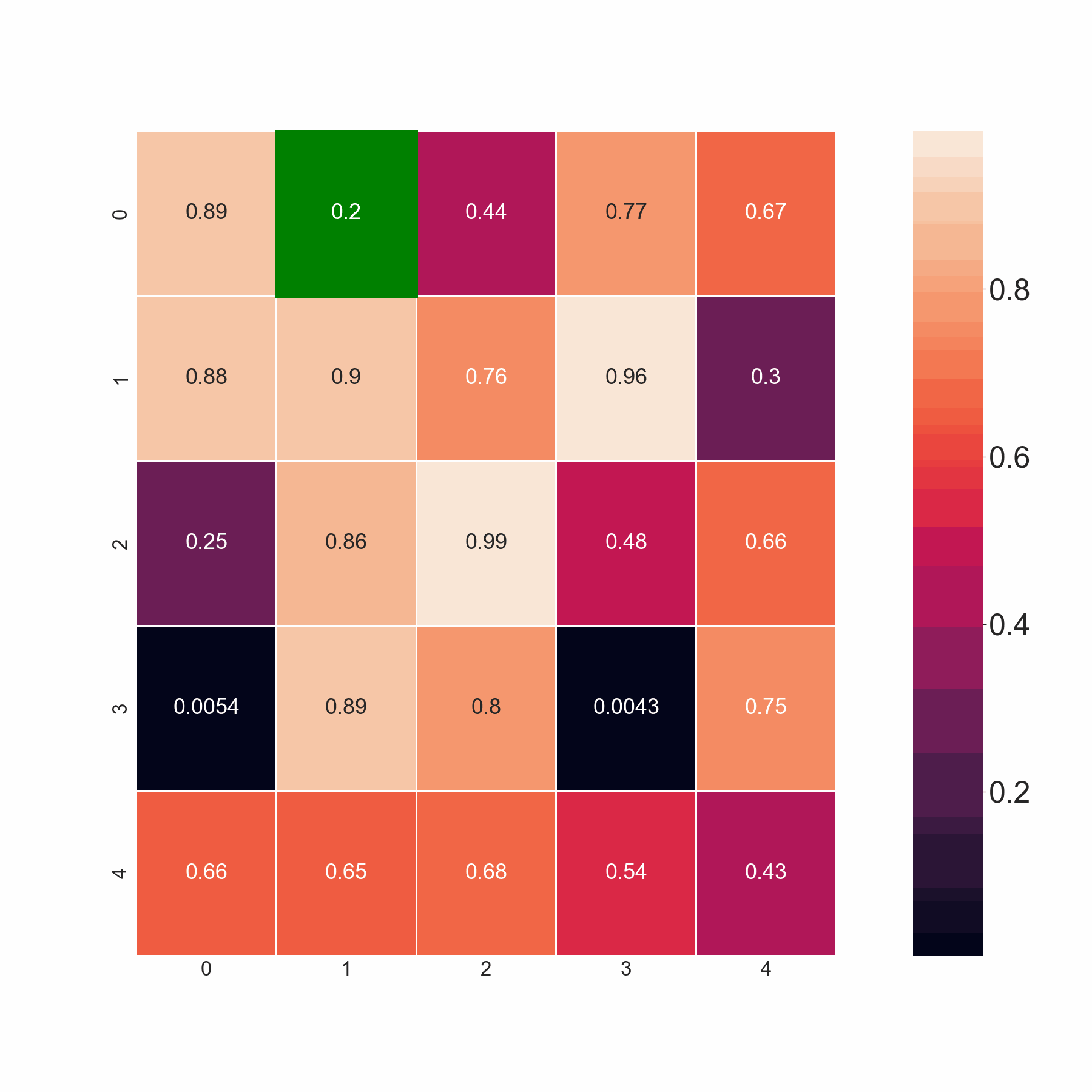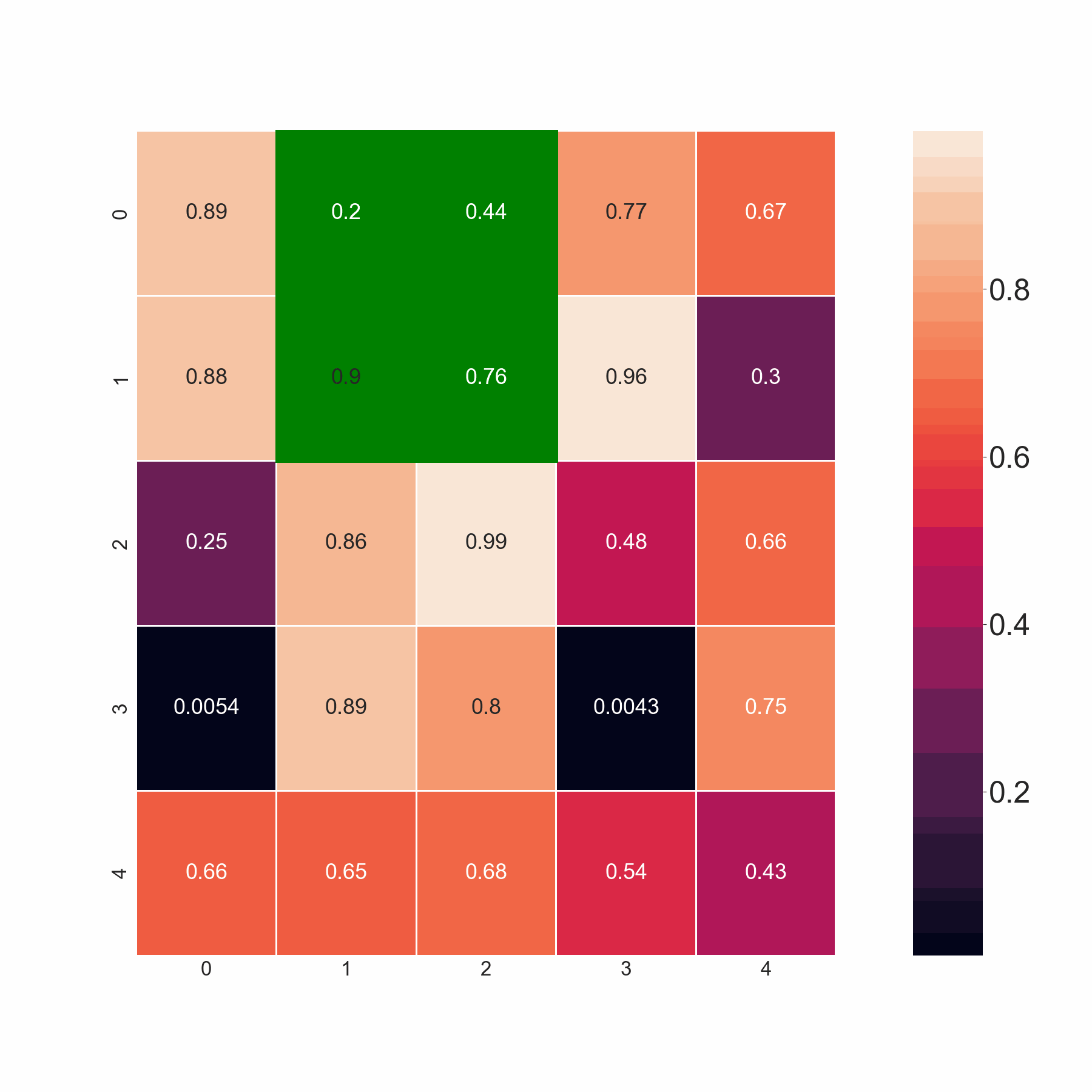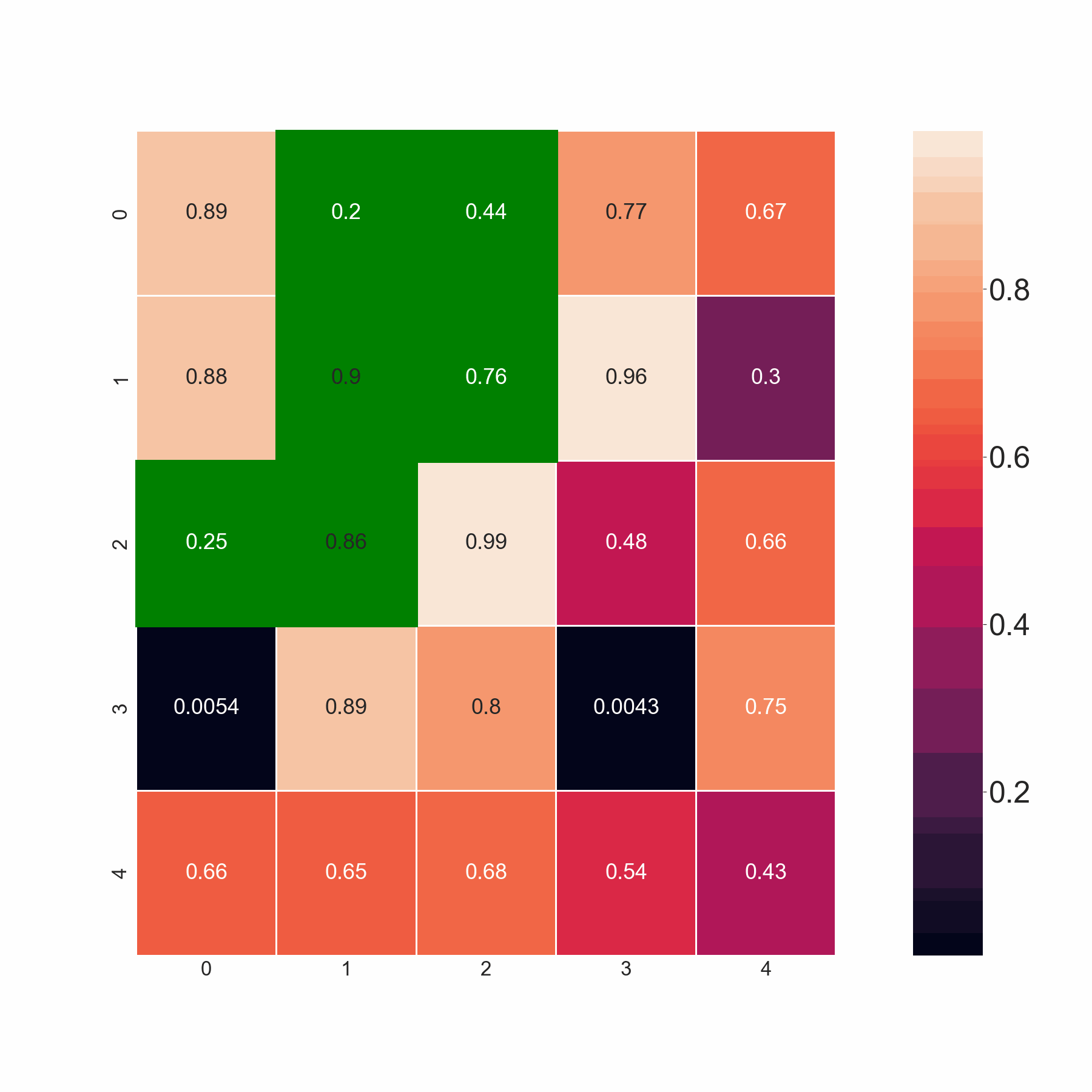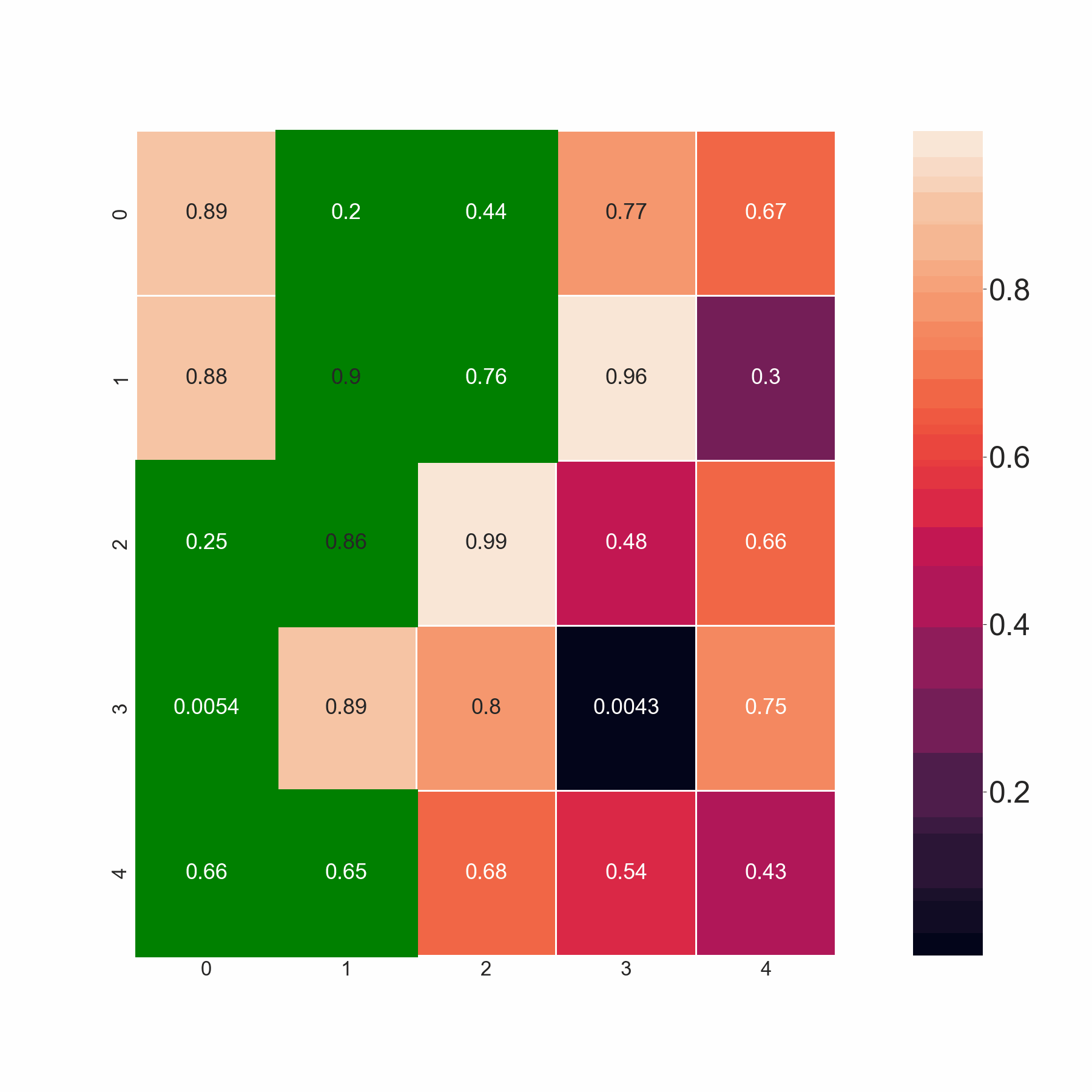
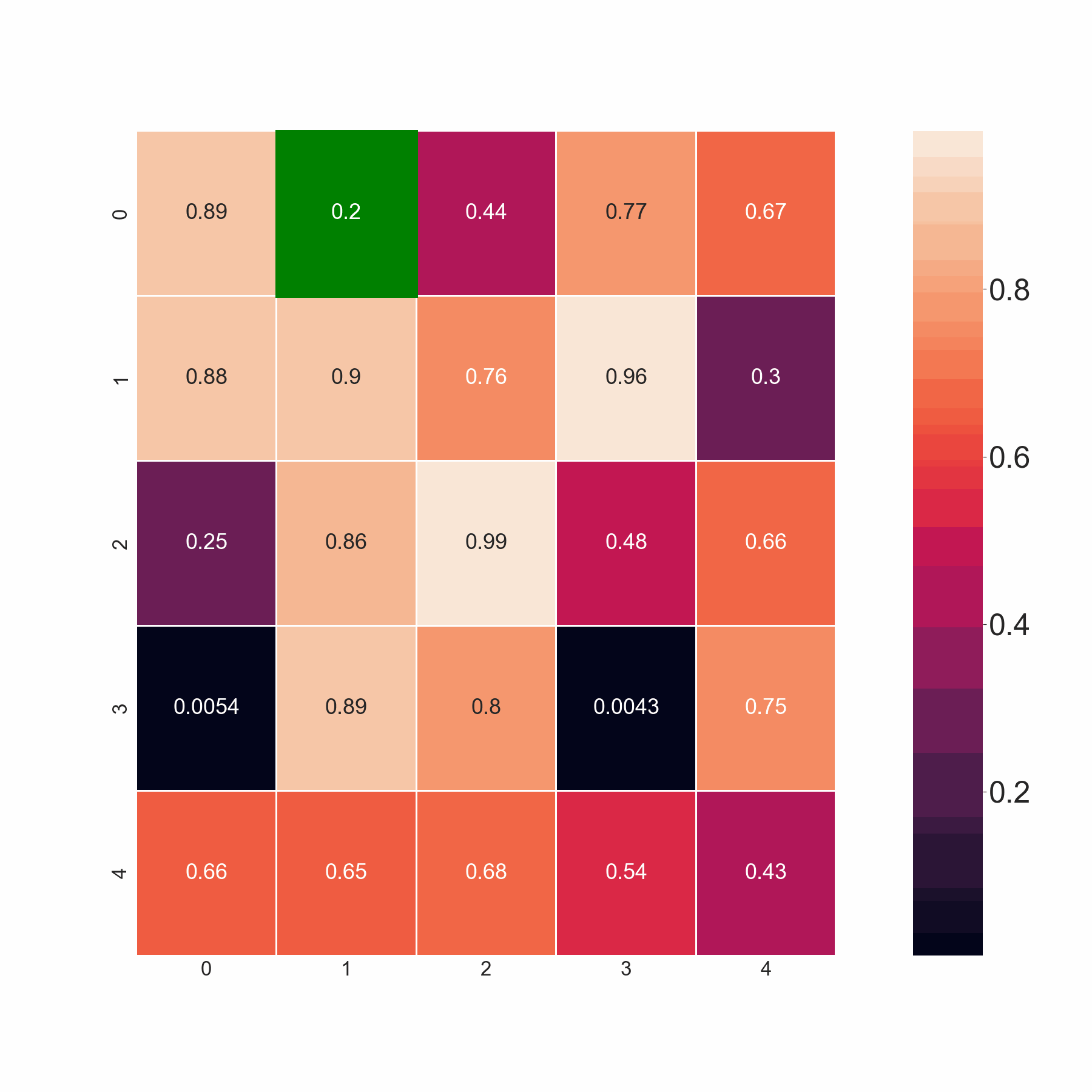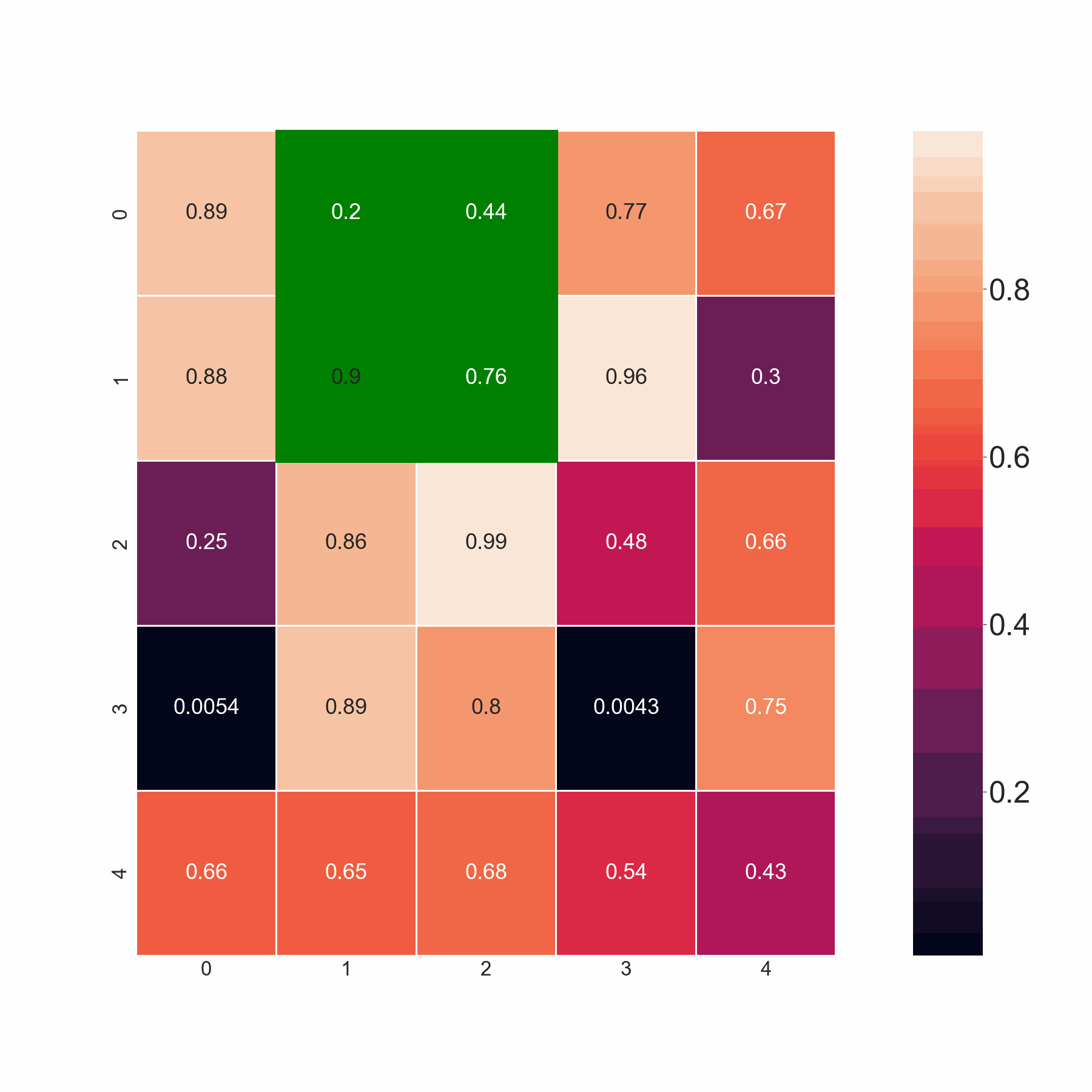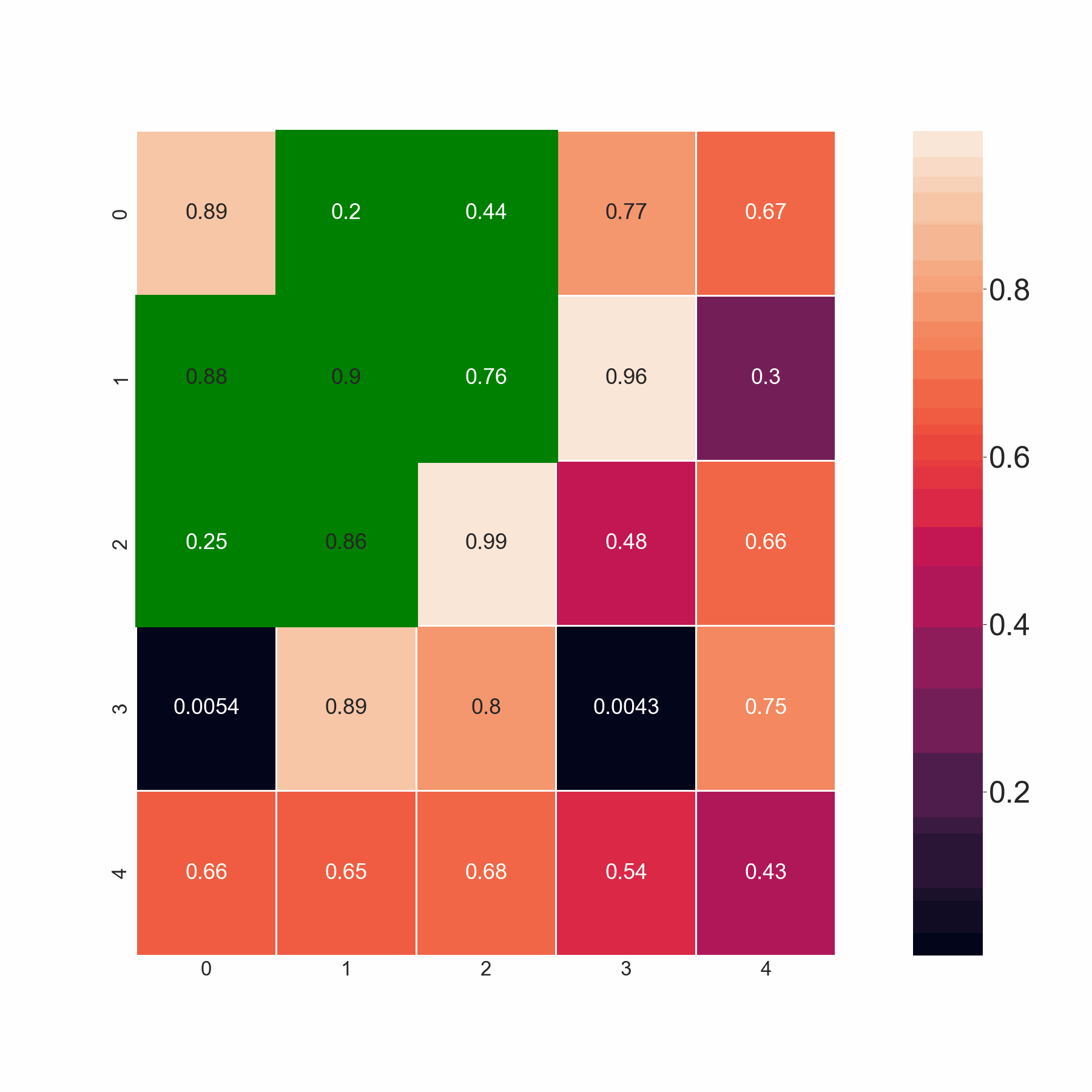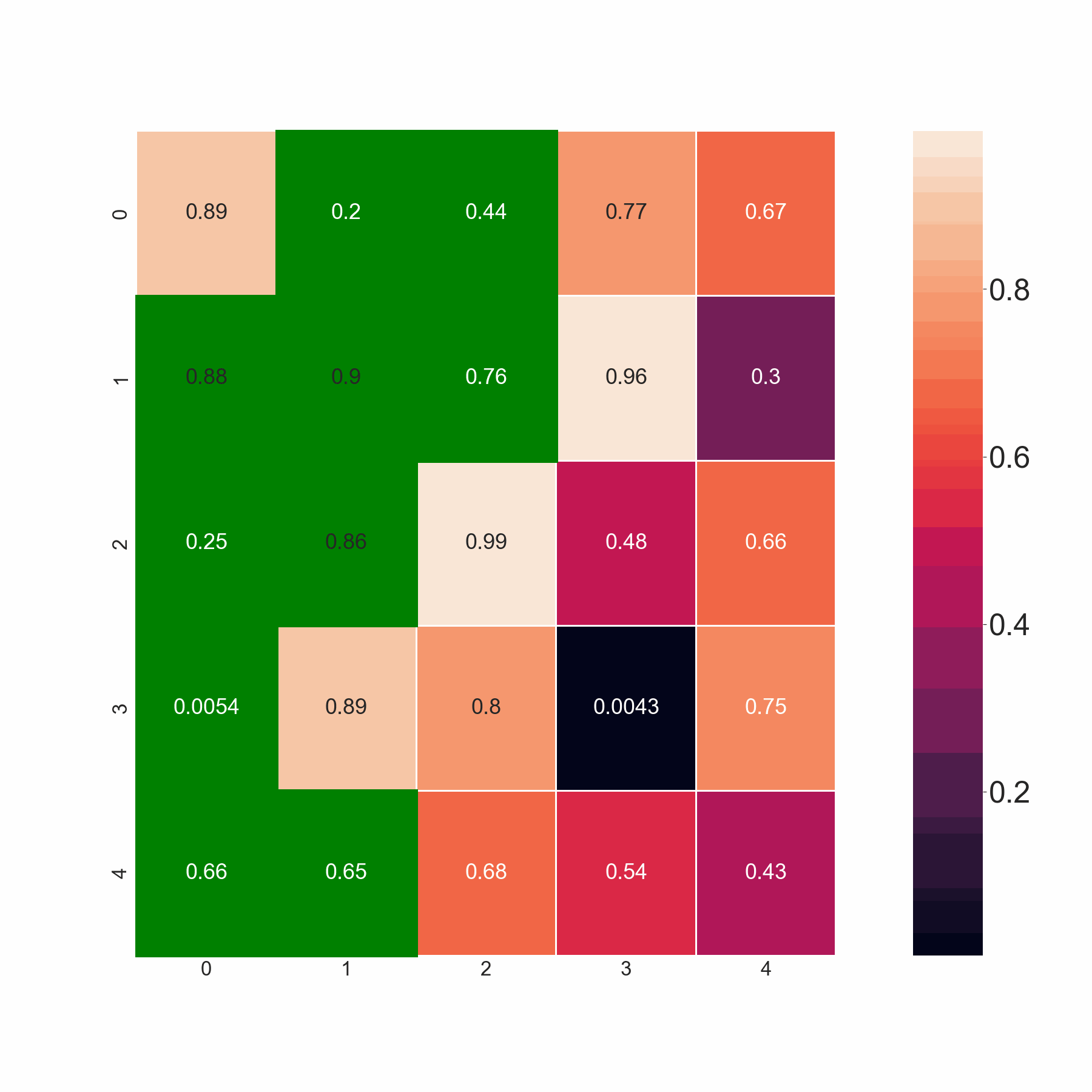
The present code selects minimum values by scanning the adjoining elements in the same and the succeeding row. However, I want the code to select all the values if they are less than the threshold value. For example, in row 2, I want the code to pick both 0.86 and 0.88 since both are less than 0.9, and not merely minimum amongst 0.86,0.88. Basically, the code should pick up the minimum value if all the adjoining elements are greater than the threshold. If that's not the case, it should pick all the values less than the threshold.

import numpy as np
import numba as nb

Pe = np.random.rand(5,5)

def minValues(arr):
    n, m = arr.shape
    assert n >= 1 and m >= 2
    res = []
    i, j = 0, np.argmin(arr[0,:])
    res.append((i, j))
    iPrev = jPrev = -1
    while iPrev < n-1:
        cases = [(i, j-1), (i, j 1), (i 1, j)]
        minVal = np.inf
        iMin = jMin = -1
        # Find the best candidate (smallest value)
        for (i2, j2) in cases:
            if i2 == iPrev and j2 == jPrev: # No cycles
                continue
            if i2 < 0 or i2 >= n or j2 < 0 or j2 >= m: # No out-of-bounds
                continue
            if arr[i2, j2] < minVal:
                iMin, jMin = i2, j2
                minVal = arr[i2, j2]
        assert not np.isinf(minVal)
        # Store it and update the values
        res.append((iMin, jMin))
        iPrev, jPrev = i, j
        i, j = iMin, jMin
    return np.array(res)

T=minValues(Pe)
Path=Pe[T.T[0], T.T[1]]

Current output:

Desired output:

CodePudding user response：

This is an interesting problem - looking at hydrology flow/downhill direction?

The issue with the description is that you don't specify which of the neighboring cells to iterate to next, meaning, if you have three neighboring cells that are lower, they all get added to the output array but which is selected? Also, when looking back through the output array how do you know which ones got added with respect to a single neighboring cell? I went about this by selecting the lowest value of the neighboring cells with less than the source cell's value (biggest dropoff), then continued the search from that cell and so on. For each iteration, there is a new nested list of the cell positions for the neighboring cells that are lower. This could readily be updated any number of ways, to include exporting an additional list showing which cells were used for search (essentially the path taken, while there might be highlighted cells (lower) that were not visited per se.

import numpy as np

Pe = np.random.rand(5,5)

def nearestMin(arr, output_arr=[[0,0]], n=0, m=0):
    if m==arr.shape[1]:
        return output_arr
    lower_vals = np.argwhere(arr < arr[n,m])
    if lower_vals.size == 0:  #No values anywhere less than current cell
        return output_arr
    #Get offset from current point, as tuple of x and y distance
    smaller_adjacents = np.where(Pe < Pe[n, m])
    if smaller_adjacents[0].size == 0:  #No lower points anywhere
        return output_arr 
    ind = np.where((abs(n - smaller_adjacents[0]) <= 1 ) & \
        (abs(m - smaller_adjacents[1]) <= 1))[0] 
    if ind.size == 0:  #No lower points neighboring
        return output_arr
    xs, ys = smaller_adjacents[0][ind], smaller_adjacents[1][ind]
    lower_neighbors = np.vstack((xs, ys)).T.tolist()
    output_arr.append(lower_neighbors) #Unbracket to have final output array be flat (2d)
    n_depth = [Pe[x,y] for x,y in lower_neighbors] - Pe[n,m]
    biggest_drop = np.where(n_depth==n_depth.min())[0][0]
    lowest_neighbor = lower_neighbors[biggest_drop]
    return nearestMin(arr, output_arr, n=lowest_neighbor[0], m=lowest_neighbor[1])

nearestMin(Pe)

CodePudding user response：

Try this:

def minValues(arr):
  n, m = arr.shape
  assert n >= 1 and m >= 2
  res = []
  i, j = 0, np.argmin(arr[0,:])
  print(f"Values i, j are: {i}, {j}")
  res.append((i, j))
  iPrev = jPrev = -1
  while iPrev < n-1:
      lowerVals = []
      print(f"Values iPrev, jPrev are: {iPrev}, {jPrev}")
      cases = [(i, j-1), (i, j 1), (i 1, j)]
      print(f"Posible cases are: {cases}")
      minVal = np.inf
      print(f"MinVal is: {minVal}")
      iMin = jMin = -1
      # Find the best candidate (smallest value)
      for (i2, j2) in cases:
          if i2 == iPrev and j2 == jPrev: # No cycles
              continue
          if i2 < 0 or i2 >= n or j2 < 0 or j2 >= m: # No out-of-bounds
              continue
          if arr[i2, j2] < arr[i, j]:
              lowerVals.append((i2, j2))
          if arr[i2, j2] < minVal:
              iMin, jMin = i2, j2
              minVal = arr[i2, j2]
      if not lowerVals: lowerVals.append((iMin, jMin))
      print(f"Values iMin, jMin are: {iMin}, {jMin}")    
      print(f"MinVal is: {minVal}")
      print(f"Lower values are: {lowerVals}")
      assert not np.isinf(minVal)
      # Store it and update the values
      res  = lowerVals
      print(f"Final res after current iteration: {res}\n")
      iPrev, jPrev = i, j
      i, j = iMin, jMin
  return np.array(res)

I used the prints for debugging, but I just check in each iteration all the values which are lower than the current value and add them to path at the end of the iteration.

Edit: introducing the extra line of my comment you get the above code, this should work.