Numerical integration for a slow converging integral-CodePudding

I basically have a problem with numerical integrations of this type:

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import quad

# Parameter
T = 94
Eps_inf = 3.05
Eps_s = 19.184544603857724
tau_0 = 1.27*10**-16
tau_CD = 0.34580390675331274
gamma = 0.49
C_pek = 1/Eps_inf - 1/Eps_s
hbar = 6.582119569*10**-16

# Functions
def func(w):
    return -4 * 1/(np.pi * C_pek) * Eps(w).imag/abs(Eps(w))**2

def Eps(w):
    return Eps_inf   (Eps_s - Eps_inf)/(1   (1j * w * tau_CD))**gamma

w = np.logspace(-9,80,100000)
y = func(w)

IntegrandS = quad(lambda w: func(w),0,np.inf,limit=100000)[0]
print(f'quadResult: {IntegrandS}')

This gives me the warning: The integral is probably divergent, or slowly convergent.

And the function is indeed slowly converging:

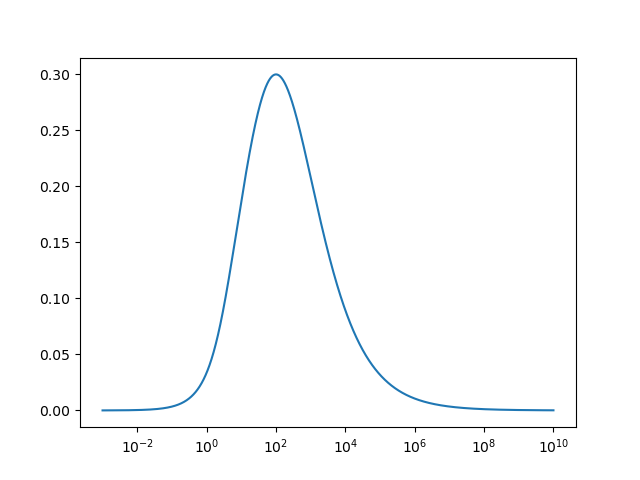
If I put in the upper limit of the integration just a big numer like 1e15 it gives me a result but that result will never converge for higher and higher integration limits.

Is there anyway to treat this function, so that the quad function (or any other integration method, i also tried scipys trapz, giving me the same problem) can deal with this function?

Thanks!

CodePudding user response：

The integral is divergent. This can be explained by looking at the asymptotic behavior of func(w) as w → ∞.

The part of func(w) that depends on w is the quotient Eps(w).imag/abs(Eps(w))**2.

As w → ∞, the real part of Eps(w) approaches Eps_inf and the imaginary part goes to 0, so as w → ∞, abs(Eps(w))**2 → Eps_inf**2. That is, the denominator approaches a positive constant. So the important part of that quotient is the numerator, Eps(w).imag.

As w → ∞, Eps(w).imag converges to 0, but that does not mean the integral of func(w) will converge. For convergence, Eps(w).imag must converge to 0 "fast enough". As w → ∞, Eps(w).imag behaves like D * w**-gamma, where D is a constant that is independent of w. An integral of the form x**p from x0 to ∞ (for some x0 > 0) is convergent only when p < -1. With your function, that power is -gamma, which is -0.49. So your function decays too slowly for the integral to converge.

You can check that if you change gamma to a value greater than 1, quad converges. E.g.

In [65]: gamma = 1.49

In [66]: quad(func, 0, np.inf)
Out[66]: (28.792185960802843, 3.501437717545741e-07)

In [67]: gamma = 1.2

In [68]: quad(func, 0, np.inf)
Out[68]: (87.82367385721193, 4.4632464835103747e-07)

In [69]: gamma = 1.01

In [70]: quad(func, 0, np.inf)
Out[70]: (2274.435541035491, 2.4941527954069898e-06)

The integral is divergent when gamma is 1. Here are two attempts to use quad in this case.

In [71]: gamma = 1.0

In [72]: quad(func, 0, np.inf)
<ipython-input-72-b9978f1fcdcd>:1: IntegrationWarning: The maximum number of subdivisions (50) has been achieved.
  If increasing the limit yields no improvement it is advised to analyze 
  the integrand in order to determine the difficulties.  If the position of a 
  local difficulty can be determined (singularity, discontinuity) one will 
  probably gain from splitting up the interval and calling the integrator 
  on the subranges.  Perhaps a special-purpose integrator should be used.
  quad(func, 0, np.inf)
Out[72]: (882.2704810872806, 188.89503399200746)

In [73]: quad(func, 0, np.inf, limit=100000)
Out[73]: (inf, inf)

When gamma < 1, quad reports (correctly) that the integral is probably divergent.

In [74]: gamma = 0.98

In [75]: quad(func, 0, np.inf, limit=100000)
<ipython-input-75-005c1a83e644>:1: IntegrationWarning: The integral is probably divergent, or slowly convergent.
  quad(func, 0, np.inf, limit=100000)
Out[75]: (-1202.853690120471, 1.0195566801485256e-05)