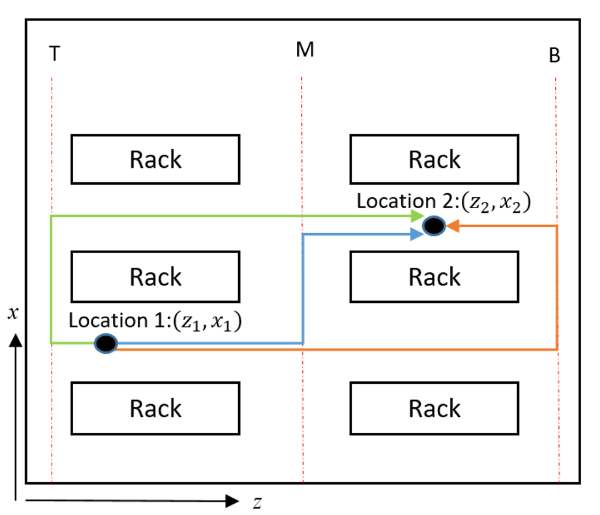
I have the layout of a warehouse with racks and aisles where items are picked from locations on the racks while traversing the aisles:

I want to compute a distance matrix between each pair of nodes/locations in the following way. Let x be the across aisle coordinate and z be the coordinate along the aisle as shown in the figure above. If x_1 = x_2 the two nodes are located on the same aisle and the distance is easily computed as t_12 = z_2-z_1 where t_12 is the distance between node 1 and 2. Otherwise, the distance between the two nodes can be calculated as follows:

t_12 = min( |z_1 - B|   |x_2 - x_1|   |z_2 - B|, |z_1 - M|   |x_2 - x_1|   |z_2 - M|, |z_1 - T|   |x_2 - x_1|   |z_2 - T|) 

since there are 3 ways to go from node 1 to node 2 and the shortest is chosen. T, M and B are the z-coordinate of top cross aisle, middle cross aisle and the bottom cross aisle.

This is what I've done so far:

import numpy as np

x_coordinates = np.linspace(0, 320, 33).astype(int)

z_coordinates = np.linspace(0, 30, 31).astype(int)

print("x coordinates = ")
print(x_coordinates)
print("z coordinates = ")
print(z_coordinates)

B = 0
M = 15
T = 31

def dist_calc(x, z):
    mat = np.zeros((len(x), len(z)))
    for i in range(len(x_coordinates)):
        for j in range(len(z_coordinates)):
            mat[i][j] = min(np.abs(z[i] - B)   np.abs(x[j] - x[j   1])   np.abs(z[i   1] - B),
                            np.abs(z[i] - M)   np.abs(x[j] - x[j   1])   np.abs(z[i   1] - M),
                            np.abs(z[i] - T)   np.abs(x[j] - x[j   1])   np.abs(z[i   1] - T))
    return mat


Distances = dist_calc(x_coordinates, z_coordinates)

I have two questions:

1. I don't see how I should incorporate the case when x_1 = x_2. I think that the way I've defined the coordinates makes it impossible to specify the condition that two nodes are on the same aisle, i.e have the same x-coordinate.

2. Of course I understand that I will get an index out of bounds error since I'm trying to access element i 1 and j 1 in arrays of length i and j respectively. Is there a way to circumvent this problem? Do I need to append an extra zero to the x and z coordinate arrays in the beginning?

CodePudding user response：

In your comment, you stated that the last point is (330,31), which is inconsistent with your linspace. The biggest mistake is that you are iterating over the individual axes, whilst you should iterate over all combinations of the coordinates. I separated out the distance calculation and the matrix generation, because generating a 1023x1023 matrix is a bit expensive.

import numpy as np

x_c = np.linspace(0, 330, 34).astype(int)
z_c = np.linspace(0, 31, 32).astype(int)

print("x coordinates = ")
print(x_c,len(x_c))
print("z coordinates = ")
print(z_c,len(z_c))
print()

B = 0
M = 15
T = 31


def dist_calc(p1,p2,B,M,T):
    return min( abs(p1[1] - B)   abs(p2[0] - p1[0])   abs(p2[1] - B) ,
                abs(p1[1] - M)   abs(p2[0] - p1[0])   abs(p2[1] - M) ,
                abs(p1[1] - T)   abs(p2[0] - p1[0])   abs(p2[1] - T) )


def gen_mat(x,z,B,M,T):
    c = [(i,j) for i in x for j in z]
    mat = np.zeros((len(c), len(c)))
    for i,p1 in enumerate(c):
        for j,p2 in enumerate(c):
                mat[i,j] = dist_calc(p1,p2,B,M,T)                   
    return mat

print('Distance between (200,31) and (150,2) should be 200-150=50;31-2=29;50 29=79')
print()

D = gen_mat(x_c,z_c,B,M,T)
c = [(i,j) for i in x_c for j in z_c]
print('By using a distance matrix:')
print(D[c.index((200,31)),c.index((150,2))])
print()

print('By using the raw distance function:')
print(dist_calc((200,31),(150,2),B,M,T))

Output:

x coordinates = 
[  0  10  20  30  40  50  60  70  80  90 100 110 120 130 140 150 160 170
 180 190 200 210 220 230 240 250 260 270 280 290 300 310 320 330] 34
z coordinates = 
[ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
 24 25 26 27 28 29 30 31] 32

Distance between (200,31) and (150,2) should be 200-150=50;31-2=29;50 29=79

By using a distance matrix:
79.0

By using the raw distance function:
79