As per Big O notations, if time complexity of one algorithm is O(2^n) and the other is O(n^1000), then which would be faster one?
CodePudding user response:
How to recognize overall behavior for some non-obvious cases: get logarithm of both functions.
(Sometimes we can also get ratio of the functions and evaluate ratio limit for large n's, here this approach is not good)
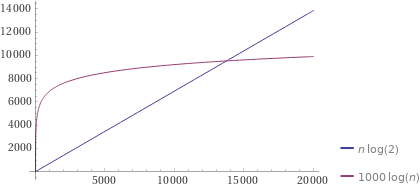
log(2^n) = n*log(2)
log(n^1000) = 1000*log(n)
The first result is slanted line with positive coefficient. The second one's plot is convex curve with negative second derivative, so the first function becomes larger at some big n value.
CodePudding user response:
For smaller number of size we encounter every day, 2^n will be smaller than O(n^1000), but if n gets large enough, in that situation it will reverse and the 2^n will start to become faster than the n^1000
CodePudding user response:
O(n^1000) is in the same class as (n^2) and O(n^777777777) which is Polynomial time, whereas O(2^n) is Exponential time which is way slower than Polynomial