I have "inherited" this code and I am not familiar with the SARIMAX model. The comments help to understand what is happening, but I do not understand the last line where the prediction is done.

The dataset has 1171 rows in total, splitted into 1000 training rows and 171 test rows. This translates to:

 Model.predict(1000, 1170, exog=exo_test, typ='levels')

I looked at the documentation for predict(). While the first parameter is the endog-parameter, the second should be the exog parameter. But when exog=exog_test, what is the 1170 supposed to mean? Also the documentation does not mention the 'typ' parameter.

What I do not understand:

1. Is this a one-step-ahead prediction? Meaning that it takes true values, predicts the next step and then discards the prediction, takes the next true value in time to predict the next?

[1. a) Wouldn't the SARIMAX Model be needed to be fitted again/retrained if it is a one-step prediction? Shouldn't the last true values be used and thus after each one-step prediction retrained on the true values?]

2. Is this multistep prediction, meaning the predictions in t 2 is based on the prediction and not the true value in t 1?

3. As I am assuming that it is one-step prediction, is it possible to "easily" transform this into a multistep prediction?

Full code:

#load dataset
df = pd.read_csv('data.csv', index_col = 'date', parse_dates = True)

#split the closing price into train and test data
train = df.iloc[:1000,4]
test = df.iloc[1000:,4]

#select exogenous variables
exo = df.iloc[:,6:61]

#split exogenuous variables into train and test data
exo_train = exo.iloc[:1000]
exo_test = exo.iloc[1000:]

#run auto_arima to find the best configuration (I selected m=7 and D=1 by running seasonal_decompose and acf and pacf plots)
auto_arima(df['close'], exogenous=exo, m=7, trace=True, D=1).summary()

#set the best configuration from auto_arima for the SARIMAX model 
Model = SARIMAX(train, exog = exo_train, order=(1,0,2), seasonal_order = (0,1,1,7))

#train model
Model = Model.fit()

#get prediction
prediction = Model.predict(len(train), len(train) len(test)-1, exog = exo_test, typ = 'levels')
 

CodePudding user response：

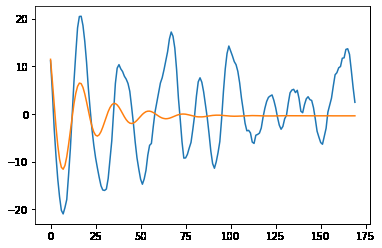
A simple exercise will show that these are dynamic predictions and so are multi-step (that is, the first is 1-step, then the 2nd is is 2-step, and so on).

#generate dataset
import matplotlib.pyplot as plt
from statsmodels.tsa.api import ArmaProcess, SARIMAX
import numpy as np
np.random.seed(20220308)

ap = ArmaProcess.from_coeffs([1.8, -0.9])
sample = ap.generate_sample(1170)

#split the closing price into train and test data
train = sample[:1000]
test = sample[1000:]

#select exogenous variables
exo = np.random.standard_normal((1170, 2))

#split exogenuous variables into train and test data
exo_train = exo[:1000]
exo_test = exo[1000:]

#set the best configuration from auto_arima for the SARIMAX model 
model = SARIMAX(train, exog = exo_train, order=(2,0,0), trend="c")

#train model
res = model.fit()

#get prediction
prediction = res.predict(len(train), len(train) len(test)-1, exog = exo_test, typ = 'levels')

x = np.arange(len(prediction))
plt.plot(x,test, x, prediction)
plt.show()

which produces

You can tell it is a multi-step since this model is stationary (an AR(2)) and the long-run forecast reverts to the unconditional mean.