from gensim.models import Word2Vec
model = Word2Vec(sentences = [['a','b'],['c','d']], window = 9999999, min_count=1)
model.wv.most_similar('a', topn=10) 

Above code gives the following result:

[('d', 0.06363436579704285),
 ('b', -0.010543467476963997),
 ('c', -0.039232250303030014)]

shouldn't the 'b' ranked first, since it's the only one nearby 'a'?

CodePudding user response：

That's an interesting question, I worked with gensim a few times and would've intuitively thought the same as you, so I looked a bit closer into it.

I think first of all you need to put in a larger number of sentences, otherwise there will be next to no effect on the trained model.

The way I understand the Word2Vec model it tries to find the similarity if words by looking at their context, so it looks at the question of the surrounding words on two words are often similar. If they are, the vector representation the model learns for these two words has a low distance from each other.

Take this example:

import random
import numpy
from gensim.models import Word2Vec


nested_list = []
for _ in range(0, 50000):
    nested_list.append(['a', 'b'])
for _ in range(0, 50000):
    nested_list.append(['c', 'd'])
for _ in range(0, 50000):
    nested_list.append(['a', 'x'])
random.shuffle(nested_list)


model = Word2Vec(sentences=nested_list, window=9999999, min_count=1)

words = ['a', 'b', 'c', 'd', 'x']
for word in words:
    print(word, model.wv.most_similar(word, topn=10))

Which will return:

a [('c', 0.11672252416610718), ('d', 0.11632005870342255), ('x', 0.09789041429758072), ('b', 0.0978466272354126)]
b [('x', 0.999595046043396), ('c', 0.10307613760232925), ('a', 0.0978466272354126), ('d', 0.09400281310081482)]
c [('a', 0.11672253161668777), ('d', 0.11085666716098785), ('b', 0.10307613760232925), ('x', 0.0969843715429306)]
d [('a', 0.11632007360458374), ('c', 0.11085667461156845), ('x', 0.10299163311719894), ('b', 0.09400279819965363)]
x [('b', 0.9995951652526855), ('d', 0.10299164056777954), ('a', 0.09789039939641953), ('c', 0.0969843715429306)]

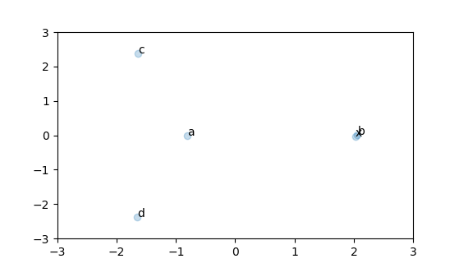
x and b often occur in a similar context (next to an a). All other distances between the representations have pretty much nothing noticable.

You can visualize that as well:

from sklearn.decomposition import PCA
import matplotlib.pyplot as plt

pca_ = PCA(n_components=2).fit_transform(numpy.array([model.wv.get_vector(v) for v in words]))
pca_x = tsne_x = [x_[0] for x_ in pca_]
pca_y = [x_[1] for x_ in pca_]
ax = plt.gca()
plt.scatter(pca_x, pca_y, alpha=0.25)
ax.set_xlim([-3, 3])
ax.set_ylim([-3, 3])
for i, name in enumerate(words):
    text = ax.annotate(name, (pca_x[i], pca_y[i]))
plt.show()

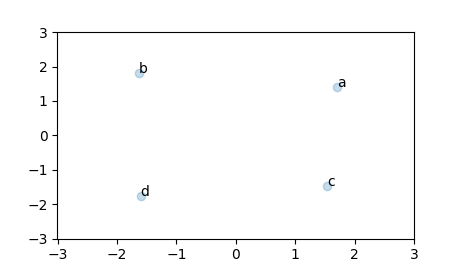
If you leave out append(['a', 'x']) loop part and remove the x from words, so remove the ['a', 'x'] sentences from the model training, you get basically just a random position with nothing noticable:

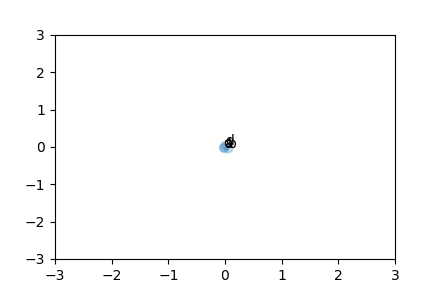
And if you replace the 50000 sentences per case with just 1:

CodePudding user response：

This algorithm only works wellwith large, varied training data.

There, subtleties of relative-cooccurrences can, via the push-and-pull of many contrasting examples, serve to nudge words into configurations that are useful, and generalizable to other texts using the same vocabulary. And most impressively to me, often match human intuitions about not just 'neighborhoods' of related words, but 'directions' of shades of meaning.

But none of those benefits are likely to be seen if you've got a toy-sized training set, or something synthetic that doesn't have the same sort of frequencies/cooccurrences as natural-language, or degenerately-simple usage examples. (Your 2-word texts, where words only have a single neighbor, and there's no chain of 'appears-close-to' relationships, however slight connecting dijoint clusters of words, are very peculiar & unnatural.)

So when trying to develop an intuitive understanding of this algorithm, I'd make sure you're always using a significant number of real natural-language texts. For example, the 100MB dataset of raw run-on text from an old Wikipedia dump known as text8 – see the text8.zip discussion about 4/5th down this page is a reasonable basis for experimentation that can roughly reproduce things like the classic king - man woman = queen result.

More generally, any time you're tempted to use min_count=1, you're probably making a mistake. There's a good reason the default of min_count=5: words with only a single (or few) usage examples won't get strong vectors via word2vec training, and further, by soaking up training time & model state, tend to worsen the vectors for surrounding suitably-represented words. (The common intution "keeping more data can only help" is backwards here.)

If you ever really want to try word2vec with a tiny amount of data, you may be able eke out a little more value with one or both of:

• Far more than the default epochs=5 - which can help give the model more chances to learn whatever's in the thin amount of text. (But note: synthetically repeating the same few examples isn't nearly as good as true variety-of-usages that a real/large dataset could offer.)
• Far fewer than the default vector_size=100 dimensions – which can prevent the model from being far larger than the training-data itself, an error which ensures overfitting.

Regarding that last point, note that in your original contrived test, you've got 2 texts of 2 words each – at most ~20 bytes of training data. But you're using that to train a model that learns 4 word-vectors of 100 4-byte float dimensions each, and also has an additional set of internal output weights equivalent to another 4 vectors of 100 4-byte float dimensions. That's a model of 3,200 bytes: 160X more internal state than would be necessary to store the whole training set.

That's a situation prone to extreme overfitting, where the model can just become a convoluted expansion of the original data, that may become arbitrarily good at modeling the idiosyncracies of the data, on the training task, without creating insights that generalize to elsewhere.

Real & effective machine learning usually looks more like compression: distilling large amounts of data down to a smaller model, which captures as much of the essence of the data, under the chosen constraints of limited size & limited methods, as possible.