I have a (potentially large) list data of 3-tuples of small non-negative integers, like

data = [
    (1, 0, 5),
    (2, 4, 2),
    (3, 2, 1),
    (4, 3, 4),
    (3, 3, 1),
    (1, 2, 2),
    (4, 0, 3),
    (0, 3, 5),
    (1, 5, 1),
    (1, 5, 2),
]

I want to order the tuples within data so that neighboring tuples (data[i] and data[i 1]) are "as similar as possible".

Define the dissimilarity of two 3-tuples as the number of elements which are unequal between them. E.g.

• (0, 1, 2) vs. (0, 1, 2): Dissimilarity 0.
• (0, 1, 2) vs. (0, 1, 3): Dissimilarity 1.
• (0, 1, 2) vs. (0, 2, 1): Dissimilarity 2.
• (0, 1, 2) vs. (3, 4, 5): Dissimilarity 3.
• (0, 1, 2) vs. (2, 0, 1): Dissimilarity 3.

Question: What is a good algorithm for finding the ordering of data which minimizes the sum of dissimilarities between all neighboring 3-tuples?

Some code

Here's a function which computes the dissimilarity between two 3-tuples:

def dissimilar(t1, t2):
    return sum(int(a != b) for a, b in zip(t1, t2))

Here's a function which computes the summed total dissimilarity of data, i.e. the number which I seek to minimize:

def score(data):
    return sum(dissimilar(t1, t2) for t1, t2 in zip(data, data[1:]))

The problem can be solved by simply running score() over every permutation of data:

import itertools
n_min = 3*len(data)  # some large number
for perm in itertools.permutations(data):
    n = score(perm)
    if n < n_min:
        n_min = n
        data_sorted = list(perm)
print(data_sorted, n_min)

Though the above works, it's very slow as we explicitly check each and every permutation (resulting in O(N!) complexity). On my machine the above takes about 20 seconds when data has 10 elements.

For completeness, here's the result of running the above given the example data:

data_sorted = [
    (1, 0, 5),
    (4, 0, 3),
    (4, 3, 4),
    (0, 3, 5),
    (3, 3, 1),
    (3, 2, 1),
    (1, 5, 1),
    (1, 5, 2),
    (1, 2, 2),
    (2, 4, 2),
]

with n_min = 15. Note that several other orderings (10 in total) with a score of 15 exist. For my purposes these are all equivalent and I just want one of them.

Final remarks

In practice the size of data may be as large as say 10000.

The sought-after algorithm should beat O(N!), i.e. probably be polynomial in time (and space).

If no such algorithm exists, I would be interested in "near-solutions", i.e. a fast algorithm which gives an ordering of data with a small but not necessarily minimal total score. One such algorithm would be

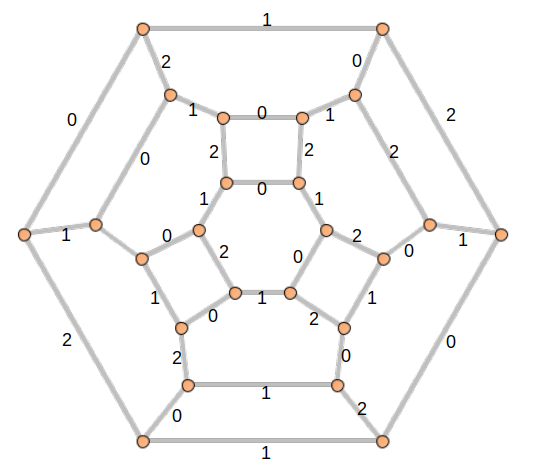
We can color the edges with colors 0, 1 and 2:

And then label the edges with minimal natural numbers L(e) that respect the colors mod 3:

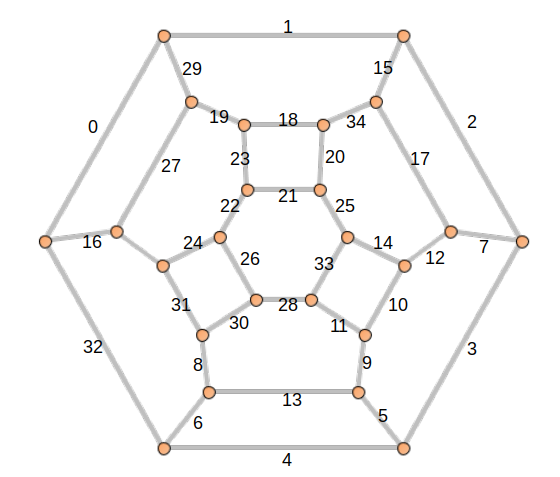
For each vertex v in V, create a 3-Tuple T = (t0, t1, t2), where t0, t1, t2 are the labels of edges incident to v with remainders equal to 0, 1, 2 respectively. Note that each edge label appears at the same index of each 3-Tuple it belongs to. In the example above, the top left vertex will get a 3-Tuple (0, 1, 29) and the left-most vertex will get a 3-Tuple (0, 16, 32).

Now, there is a Hamiltonian path in G if and only if there is an ordering of 3-Tuples with dissimilarity sum
2 * (|V| - 1). This is because an ordering of 3-Tuples has that dissimilarity sum if and only if the ordering corresponds to a Hamiltonian path in G.

CodePudding user response：

This isn't exact algorithm, just heuristic, but should be better that naive sorting:

out = [data.pop(0)]
while data:
    idx, t = min(enumerate(data), key=lambda k: dissimilar(out[-1], k[1]))
    out.append(data.pop(idx))


print(score(out))

Testing (100 repeats with data len(data)=1000):

import random
from functools import lru_cache


def get_data(n=1000):
    f = lambda n: random.randint(0, n)
    return [(f(n // 30), f(n // 20), f(n // 10)) for _ in range(n)]


@lru_cache(maxsize=None)
def dissimilar(t1, t2):
    a, b, c = t1
    x, y, z = t2
    return (a != x)   (b != y)   (c != z)


def score(data):
    return sum(dissimilar(t1, t2) for t1, t2 in zip(data, data[1:]))


def lexsort(data):
    return sorted(data)


def heuristic(data):
    data = data[:]
    out = [data.pop(0)]
    while data:
        idx, t = min(enumerate(data), key=lambda k: dissimilar(out[-1], k[1]))
        out.append(data.pop(idx))
    return out


N, total_lexsort, total_heuristic = 100, 0, 0
for i in range(N):
    data = get_data()
    r1 = score(lexsort(data))
    r2 = score(heuristic(data))
    print("lexsort", r1)
    print("heuristic", r2)

    total_lexsort  = r1
    total_heuristic  = r2

print("total score lexsort", total_lexsort)
print("total score heuristic", total_heuristic)

Prints:

...

total score lexsort 178169
total score heuristic 162568