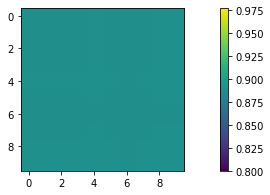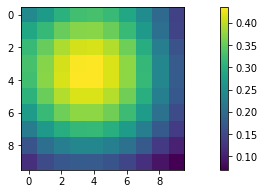I'm using flow = cv2.calcOpticalFlowFarneback() to calculate optical flow in a video and it gives me a numpy array with a shape of (height, width, 2) that contains the Fx and Fy values for each pixel (flow[:,:,0] = Fx and flow[:,:,1] = Fy).

For calculating the divergence I'm using np.gradient like this:

def divergence_npgrad(flow):
    Fx, Fy = flow[:, :, 0], flow[:, :, 1]
    F = [Fx, Fy]
    d = len(F)
    return np.ufunc.reduce(np.add, [np.gradient(F[i], axis=i) for i in range(d)])

Next, I want to calculate the curl. I know there is a curl function in sympy.physics.vector but I really don't get how is it working or how is it would apply to my flow. So I thought I could use np.gradient for this too. In 2D I need to calculate dFy/dx - dFx/dy for every pixel, so i wold be like this:

def curl_npgrad(flow):
    Fx, Fy = flow[:, :, 0], flow[:, :, 1]
    dFx_dy = np.gradient(Fx, axis=1)
    dFy_dx = np.gradient(Fy, axis=0)
    curl = np.ufunc.reduce(np.subtract, [dFy_dx, dFx_dy])
    return curl

Is it a right way to do this or am I missing something?

Now if I have the curl, I want to make two plots with matplotlib. My point is that I want to show the vectors from flow with different colormaps. One plot would use the magnitude values of the vectors as colormap, normalized to (0-magnitude_max). The other plot would use the curl values as colormap, where the arrows are blue if the curl is negative and red if the curl is positive in that position.

Here is what I'm trying to use:

def flow_plot(flow, frame):
    frame = cv2.cvtColor(frame, cv2.COLOR_BGR2RGB)
    h, w = flow.shape[:2]
    dpi = 72
    xinch = w / dpi
    yinch = h / dpi

    step = 24

    y, x = np.mgrid[step / ((h % step) // 2):h:step, step / ((w % step) // 2):w:step].reshape(2, -1).astype(int)
    fx, fy = flow[y, x].T
    mag = np.sqrt(np.power(fx, 2)   np.power(fy, 2))
    fx = fx / mag
    fy = fy / mag

    curl = curl_npgrad(flow)
    curl_map = curl[y, x]

    quiver_params = dict(cmap='Oranges', # for magnitude
                         #cmap='seismic', # for curl
                         norm=colors.Normalize(vmin=0.0, vmax=1.0), # for magnitude
                         #norm = colors.CenteredNorm(), # for curl
                         units='xy',
                         scale=0.03,
                         headwidth=3,
                         headlength=5,
                         minshaft=1.5,
                         pivot='middle')

    fig = plt.figure(figsize=(xinch, yinch), dpi=dpi)
    plt.imshow(frame)
    plt.quiver(x, y, fx, fy, mag, **quiver_params)
    plt.gca().invert_yaxis()
    plt.gca().set_aspect('equal', 'datalim')
    plt.axis('off')
    fig.tight_layout(pad=0)
    fig.canvas.draw()
    img = np.frombuffer(fig.canvas.tostring_rgb(), dtype='uint8')
    img = img.reshape(fig.canvas.get_width_height()[::-1]   (3,))
    img = cv2.cvtColor(img, cv2.COLOR_RGB2BGR)
    img = cv2.flip(img, 0)
    plt.close(fig)
    return img

I'm converting the plot to a cv2 image so i can use it for opencv video writer.

I noticed that if I'm not showing the original frame behind the plot, I have to invert the y axis and use -fy in plt.quiver(), if I want to show the frame behind, I have to invert the y axis too, can use fy, but than I have to flip the whole image afterwards. How does it make any sense? I can't get it.

As for the curl, it's kinda messy for me. barely showing any color, random red an blue spots, not a buch of red/blue arrows where the fluid clearly rotating. It's like these:

For this function, divergence should be high everywhere. Applying your function, it tells me that divergence is 0.

Code to produce this array:

import numpy as np
import matplotlib.pyplot as plt

x,y = np.meshgrid(np.linspace(-2,2,10),np.linspace(-2,2,10))

u = x
v = y
field2 = np.stack((u, v), axis=-1)

plt.quiver(x, y, field2[:, :, 0], field2[:, :, 1])

I also tried a function for testing curl:

F_x = cos(x   y)
F_y = sin(x - y)

Which produces this plot:

Code to produce this array:

import numpy as np
import matplotlib.pyplot as plt

x,y = np.meshgrid(np.linspace(0,2,10),np.linspace(0,2,10))

u = np.cos(x   y)
v = np.sin(x - y)
field = np.stack((u, v), axis=-1)

plt.quiver(x, y, field[:, :, 0], field[:, :, 1])

_{Thanks to}

Result: positive, constant value everywhere.