Testing how faster/slower are commands in R-CodePudding

I am trying to figure out how fast/slow each of the following operations are for calculating the cumulative sum from 1 to 100.

install.package('microbenchmark')
library(microbenchmark)

#Method 1
cs_for = function(x) {
  for (i in x) {
    if (i == 1) {
      xc = x[i]
    } else {
      xc = c(xc, sum(x[1:i]))
    }
  }
  xc
}

cs_for(1:100)

# Method 2: with apply (3 lines)
cs_apply = function(x) {
  sapply(x, function(x) sum(1:x))
}

cs_apply(100)

# Method 3: 
cumsum (1:100)

microbenchmark(cs_for(1:100), cs_apply(100), cumsum(1:100))

The output I get is the following one:

Unit: nanoseconds
          expr   min     lq      mean   median     uq    max neval cld
 cs_for(1:100) 97702 100551 106129.05 102500.5 105151 199801   100   c
 cs_apply(100)  8700   9101  10639.99   9701.0  10651  54201   100  b 
 cumsum(1:100)   501    701    835.96    801.0    801   3201   100 a

This shows that the last method has the highest rank of efficiency in comparison to the other two. Just in the case, I am interested how much each method is faster (both in percentage and as a number of times it is faster), I would like to know which kind of operation you suggest to apply?

CodePudding user response：

Be careful that you benchmark the correct thing: cs_appy(100) isn’t the same as cs_for(100)! It’s a shame that ‘microbenchmark’ doesn’t warn you of this. By contrast, the ‘bench’ package does:
```
bench::mark(cs_for(1 : 100), cs_apply(100), cumsum(1 : 100))
# Error: Each result must equal the first result:
# `cs_for(1:100)` does not equal `cs_apply(100)`
```
Be careful that your benchmark is representative: you are looking at a single data point (input of length 100), and it’s a tiny input size. The results are very likely to be dominated by noise, even with repeat measurements.
Always benchmark with several different input sizes to get an idea of the asymptotic growth. In fact, your question “how many times” one method is faster than the other doesn’t even make sense, because the different functions do not have the same asymptotic behaviour: two are linear, and one is quadratic. To see this, you must measure repeatedly. ‘microbenchmark’ doesn’t support this out of the box, but ‘bench’ does (but you could of course do it manually).
To perform an apples-to-apples comparison, the cumsum() benchmark should also be wrapped inside a function, and all functions should accept the same parameter (I suggest n, the size of the input vector).

Putting this all together, and using the ‘bench’ package, we get the following. I also added a benchmark using ‘vapply’, since that’s generally preferred to sapply:

cs_for = function (n) {
  x = 1 : n
  for (i in x) {
    if (i == 1L) {
      xc = x[i]
    } else {
      xc = c(xc, sum(x[1 : i]))
    }
  }
  xc
}

cs_apply = function (n) {
  sapply(1 : n, \(x) sum(1 : x))
}

cs_vapply = function (n) {
  vapply(1 : n, \(x) sum(1 : x), integer(1L))
}

cs_cumsum = function (n) {
  cumsum(1 : n)
}

results = bench::press(
    n = 10L ^ (1 : 4), # from 10 to 10,000
    bench::mark(cs_for(n), cs_apply(n), cs_vapply(n), cs_cumsum(n))
)

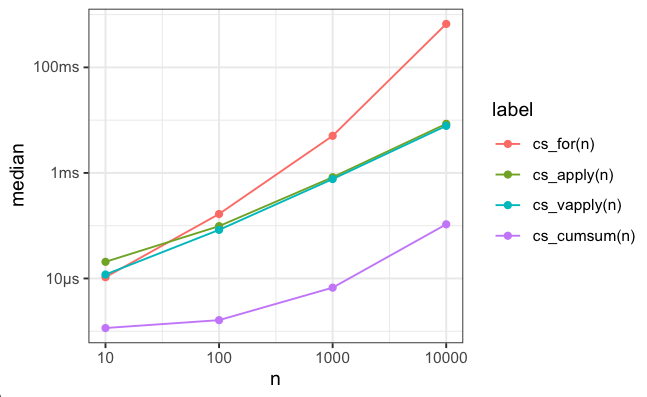
And since the first rule of data science is “visualise your results”, here’s a plot:

results |>
  mutate(label = reorder(map_chr(expression, deparse), desc(median))) |>
  ggplot()  
  aes(x = n, y = median, color = label)  
  geom_line()  
  geom_point()  
  bench::scale_y_bench_time()  
  scale_x_log10()

… As you can see, not all lines increase linearly. In fact, both cs_for and cs_cumsum increase super-linearly. cs_for has quadratic runtime because progressively appending to the xc vector necessitates allocating new storage and copying over the old values. Both apply and vapply avoid this. You can also avoid this when using for by pre-allocating your result vector. The fact that cumsum also exhibits super-linear runtime actually surprises me — it definitely shouldn’t do that! This merits further investigation.

CodePudding user response：

You can work with the table of results by saving the summary:

results <- summary(microbenchmark(cs_for(1:100), cs_apply(100), cumsum(1:100)))

It's then straigtforward to do calculations on is such as working out how many times the median time is greater than the fastest median with:

results[,"median"]/min(results[,"median"])
# [1] 131.35714  14.14286   1.00000