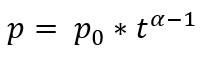Problem implementing an equation into an animation-CodePudding

I'm using the following code to simulate the motion of a set of particles, where a parameter p determines the probability of a given particle to move or not, and generates an animated plot:

# Comparação entre random walk e difusão em 1d
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
import matplotlib.patches as mpatches
import random

M = 100 # Número de walkers
L = 50 # Tamanho da malha

# A cada intervalo de tempo, mover o walker e propagar a difusão

p = 0.22 # Probabilidade de andar, difusividade em μm²/s
pinv = 1.0-p
nsteps = 2001 # Número de intervalos de tempo

# Iniciando os walkers

x = np.zeros(M) # Posição inicial dos walkers nos eixos x, y e z
Z = [(0,0,0) for i in range (M)]
edgesrw = np.array(range(-L,L 1))-0.5
xc = 0.5*(edgesrw[:-1] edgesrw[1:])

#%%

def animate(it):
    global x
    x = get_data(Z, M)

    # Trajetória dos walkers nos eixos x, y e z
    if (np.mod(it,noutput)==0):
        A = np.float64(Z)
        plot._offsets3d = (A[:,0], A[:,1], A[:,2])
        ax.set_title('Tempo = {}, p = {}'.format(it, str(round(p, 4))))
    return plot

def get_data(Z, M):
    # Atualizar a posição de todos os walkers
    for iw in range(M):
        rndx = random.random()
        dx = -1*(rndx<p) 1*(rndx>pinv)
        rndy = random.random()
        dy = -1*(rndy<p) 1*(rndy>pinv)
        rndz = random.random()
        dz = -1*(rndz<p) 1*(rndz>pinv)
        x, y, z = Z[iw]
        Z[iw] = x dx, y dy, z dz
    return Z

plt.ion()
noutput = 5
fig = plt.figure()
ax = fig.add_subplot(111, projection = '3d')
fig.set_size_inches(6, 6)
ax.set_xlim((-50, 50))
ax.set_ylim((-50, 50))
ax.set_zlim((-50, 50))
ax.set_xlabel('Distância percorrida (x)')
ax.set_ylabel('Distância percorrida (y)')
ax.set_zlabel('Distância percorrida (z)')
subs1 = mpatches.Patch(color = 'blue', label = "Ca²\u207A")
ax.legend(handles = [subs1])

x = get_data(Z, M)
plot = ax.scatter (*zip(*Z), marker = 'o', s = 3, color = 'blue')
          
ani = animation.FuncAnimation(fig = fig, func = animate, frames = nsteps, interval = 50)
ani.save('Íons Ca2 , Dab constante.gif')
plt.show()

Right now, p is a constant value. This code gives me the following result:

What I want to do now is, instead of always using p as a constant value, update it over time using the following equation:

Where p0 is the constant value from before, t is the time (counted by the parameter it in the code) and alpha is another constant value. I know that this equation won't work when t is equal to zero, and in this case I'll consider p being equal to p0.

So, I defined p0 and alpha, as well as the conditional that will verify if it is equal to zero or not, and then decide what to do:

# Comparação entre random walk e difusão em 1d
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
import matplotlib.patches as mpatches
import random

M = 100 # Número de walkers
L = 50 # Tamanho da malha

# A cada intervalo de tempo, mover o walker e propagar a difusão

p = 0.22 # Probabilidade de andar, difusividade em μm²/s
p0 = 0.22
pinv = 1.0-p
nsteps = 2001 # Número de intervalos de tempo
alpha = 0.76 # Slope da curva experimental

# Iniciando os walkers

x = np.zeros(M) # Posição inicial dos walkers nos eixos x, y e z
Z = [(0,0,0) for i in range (M)]
edgesrw = np.array(range(-L,L 1))-0.5
xc = 0.5*(edgesrw[:-1] edgesrw[1:])

#%%

def animate(it):
    global x
    x = get_data(Z, M)

    # Trajetória dos walkers nos eixos x, y e z
    if (np.mod(it,noutput)==0):
        if it == 0:
            p = p0
        else:
            p = p0*it**(alpha-1)
            pinv = 1.0-p
        A = np.float64(Z)
        plot._offsets3d = (A[:,0], A[:,1], A[:,2])
        ax.set_title('Tempo = {}, p = {}'.format(it, str(round(p, 4))))
    return plot

def get_data(Z, M):
    # Atualizar a posição de todos os walkers
    for iw in range(M):
        rndx = random.random()
        dx = -1*(rndx<p) 1*(rndx>pinv)
        rndy = random.random()
        dy = -1*(rndy<p) 1*(rndy>pinv)
        rndz = random.random()
        dz = -1*(rndz<p) 1*(rndz>pinv)
        x, y, z = Z[iw]
        Z[iw] = x dx, y dy, z dz
    return Z

plt.ion()
noutput = 5
fig = plt.figure()
ax = fig.add_subplot(111, projection = '3d')
fig.set_size_inches(6, 6)
ax.set_xlim((-50, 50))
ax.set_ylim((-50, 50))
ax.set_zlim((-50, 50))
ax.set_xlabel('Distância percorrida (x)')
ax.set_ylabel('Distância percorrida (y)')
ax.set_zlabel('Distância percorrida (z)')
subs1 = mpatches.Patch(color = 'blue', label = "Ca²\u207A")
ax.legend(handles = [subs1])

x = get_data(Z, M)
plot = ax.scatter (*zip(*Z), marker = 'o', s = 3, color = 'blue')
          
ani = animation.FuncAnimation(fig = fig, func = animate, frames = nsteps, interval = 50)
ani.save('Íons Ca2 , alpha = {}.gif'.format(alpha))
plt.show()

But I'm pretty sure the placement of this is wrong, because I'm not having the intended result (I expected the overall spread of the particles to be decreased, since p is supposed to decrease over time according to the equation).

CodePudding user response：

The variables p and pinv inside the animate functions are local to animate: it means that the values you computed for p and pinv inside this function are not going to be "shared" globally. As a consequence, every time you call get_data(Z, M) from inside animate, you are computing new data with the initial global values of p and pinv.

Here I modified get_data to receive updated values. Also note that I have changed the order of commands inside animate:

# Comparação entre random walk e difusão em 1d
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
import matplotlib.patches as mpatches
import random

M = 100 # Número de walkers
L = 50 # Tamanho da malha

# A cada intervalo de tempo, mover o walker e propagar a difusão

p = 0.22 # Probabilidade de andar, difusividade em μm²/s
p0 = 0.22
pinv = 1.0-p
nsteps = 2001 # Número de intervalos de tempo
alpha = 0.76 # Slope da curva experimental

# Iniciando os walkers

x = np.zeros(M) # Posição inicial dos walkers nos eixos x, y e z
Z = [(0,0,0) for i in range (M)]
edgesrw = np.array(range(-L,L 1))-0.5
xc = 0.5*(edgesrw[:-1] edgesrw[1:])

#%%

def animate(it):
    global x
    
    # Trajetória dos walkers nos eixos x, y e z
    if (np.mod(it,noutput)==0):
        if it == 0:
            p = p0
        else:
            p = p0*it**(alpha-1)
        pinv = 1.0-p
        
        x = get_data(Z, M, p, pinv)
        A = np.float64(Z)
        plot._offsets3d = (A[:,0], A[:,1], A[:,2])
        ax.set_title('Tempo = {}, p = {}'.format(it, str(round(p, 4))))

def get_data(Z, M, p, pinv):
    # Atualizar a posição de todos os walkers
    for iw in range(M):
        rndx = random.random()
        dx = -1*(rndx<p) 1*(rndx>pinv)
        rndy = random.random()
        dy = -1*(rndy<p) 1*(rndy>pinv)
        rndz = random.random()
        dz = -1*(rndz<p) 1*(rndz>pinv)
        x, y, z = Z[iw]
        Z[iw] = x dx, y dy, z dz
    return Z

plt.ion()
noutput = 5
fig = plt.figure()
ax = fig.add_subplot(111, projection = '3d')
fig.set_size_inches(6, 6)
ax.set_xlim((-50, 50))
ax.set_ylim((-50, 50))
ax.set_zlim((-50, 50))
ax.set_xlabel('Distância percorrida (x)')
ax.set_ylabel('Distância percorrida (y)')
ax.set_zlabel('Distância percorrida (z)')
subs1 = mpatches.Patch(color = 'blue', label = "Ca²\u207A")
ax.legend(handles = [subs1])

x = get_data(Z, M, p, pinv)
plot = ax.scatter (*zip(*Z), marker = 'o', s = 3, color = 'blue')
          
ani = animation.FuncAnimation(fig = fig, func = animate, frames = nsteps, interval = 50)
# ani.save('Íons Ca2 , alpha = {}.gif'.format(alpha))
plt.show()