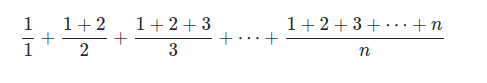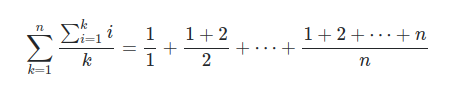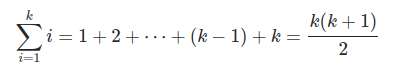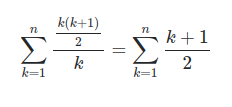Python: calculate (1/1) (1 2) / 2 ... (1 2 ... n) / n-CodePudding

The use of for loops is not allowed. This program is designed to calculate values up to number 'n' which is a value entered by the user. Help on this would be appreciated. A photo of the problem and my code so far is listed below:

import math

counterN = 0 #Numerator
counterD = 0 #Denominator
divNumber = 0 #Numerator/Denominator
nValue = 0  #Variable to add numberator values to
dValue = 0  #Variable to add denominaor values to

#Prompts user for a 
print("Please enter a value for calculation: ")
number = int(input())
if (number <= 0):
    print("Invalid input given.")

#Adds the numerator up to number entered by user
while (counterN <= number):
    counterN = counterN   1
    nValue  = counterN
    #Denominator calculation
    counterD = counterD   1
    dValue  = counterD
    divNumber = nValue / dValue
    divNumber  = divNumber


#Outputs value to user
print("The result is" , divNumber)
print(counterN, nValue)

CodePudding user response：

You can use recursion for such problems. I've written a recursive solution for you which I found very intuitive-

global SUM
SUM = 0

def fracSUMCalc(n):
    if n == 1:
        return 1
    SUM = fracSUMCalc(n-1)   (sum(range(1, n 1)) / n)
    return SUM

print(fracSUMCalc(n=998))

This prints out 249749.5 which is the answer to the sum of your series till n=998. You can vary n as per your need.

Please note that this solution will work fine on any standard modern day laptop till n=998. For n>998, you'd either have to increase your machine's recursion depth limit or use a different approach to develop a more efficient program.

CodePudding user response：

There is a solution that just uses no loops or recursion at all, just maths

def frac_series_sum(n):
    return n   sum(range(n)) * 0.5

print(frac_series_sum(1)) # 1.0
print(frac_series_sum(5)) # 10.0
print(frac_series_sum(100)) # 2575.0

CodePudding user response：

Bro, I just did easier, you could use math.factorial

import math

counterN = 1 #Numerator
result = []

#Prompts user for a 
print("Please enter a value for calculation: ")
number = int(input())

if (number <= 0):
    print("Invalid input given.")

#Adds the numerator up to number entered by user
while (counterN <= number):

    numerator = math.factorial(counterN)

    denominator = counterN

    result.append(numerator / denominator)
    #solucion
    counterN  = 1


#Outputs value to user
print("The result is" , sum(result))

CodePudding user response：

Given a number n entered by the user, this function calculates the sum you want. It does not involve any recursion, for loops or any kind of iteration (it is O(1)):

def my_calc(n):
    "Returns 1/1   (1   2)/2   ...   (1   2   ...   n)/n"
    return 0.25 * n * (n   3)

This is as efficient as it gets (see below for how I arrived at it).

If for whatever reason you are not allowed to use the solution above and you need to use a while loop:

def my_inefficient_calc(n):
    "Returns 1/1   (1   2)/2   ...   (1   2   ...   n)/n"
    result = 0
    i = 1
    while (i <= n):
        result  = (sum(range(1, i   1))) / i
        i  = 1
    return result

And if for whatever reason you are not allowed to use the built-in sum function, you can calculate the sum using a nested while loop:

def even_less_efficient(n):
    "Returns 1/1   (1   2)/2   ...   (1   2   ...   n)/n"
    result = 0
    i = 1
    while (i <= n):
        inner_sum = 0
        k = 1
        while (k <= i):
            inner_sum  = k
            k  = 1
        result  = inner_sum / i
        i  = 1
    return result

i is a loop variable (counter) for the outer loop. It ranges from i = 1 up to n.
k is a loop variable (counter) for the inner loop. It ranges from k = 1 up to i.
The inner loop is responsible for calculating the sum in the numerator for each term. This sum is stored in inner_sum.
Once the sum is calculated for a given i (i.e. once we are done with the inner loop), we divide this sum by i to get one of the terms in the mathematical expression.
The outer loop is responsible for summing all of the terms from i = 1 up to n.

Intuitive Proof

How did I arrive at this?

You want a program that calculates the following sum:

This is an elegant solution that has stuck with me for a long time that I will never forget. I once learned in real analysis of a famous mathematician who at the age of 5 (if I remember correctly) reasoned that the sum of i from i = 1 up to k is:

He did so by writing out the sum twice, but the second in reverse order:

(sum of i from i = 1 to k) = 1   2         ...   (k - 1)   k
(sum of i from i = 1 to k) = k   (k - 1)   ...   2         1
----------------------------------------------------------
                          (k 1)  (k 1)    ...    (k 1)     (k 1)  # k terms

He noticed that each sum has k numbers and the sum of each column is equal to k 1. So, if you add the two sums, you get

2 * (sum of i from i = 1 to k) = k * (k   1)

Thus

(sum of i from i = 1 to k) = (k * (k   1)) / 2

which is the same as the result in the second image above.

Substitution of this result into the left-hand-side of the expression in the first image:

Now, simplify this sum and apply the result that we derived (again):

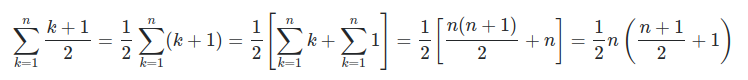
noticing that 1 is simply 2 divided by 2 and simplifying, we find out that the sum is

0.25 * n * (n   3)