Plot surface where Z depends on a vector of X and Y-CodePudding

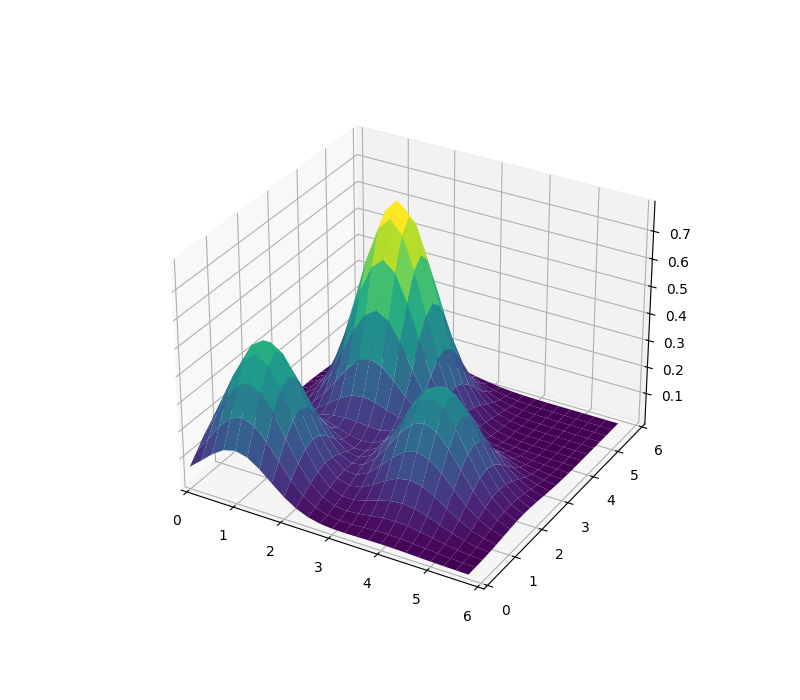
I'm currently working on a small python script which can be used to interpolate points with a radial basis function approach. Therefore I would like to plot a surface where the Z value is calculated by a vector which depends on X and Y.

The formula I need to implement looks like this:

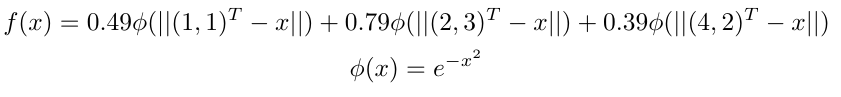
My current approach is the following:

import numpy as np
import matplotlib.pyplot as plt 

def phi(x):
    return np.exp(- np.power(x, 2))

fig = plt.figure(figsize=(8,7))
ax = fig.add_subplot(projection='3d')

x = np.arange(0, 6, 0.25)
y = np.arange(0, 6, 0.25)
X, Y = np.meshgrid(x, y)

Z = 0.49 * phi(np.linalg.norm(np.array([[1,1], [X,Y]])))   \
    0.79 * phi(np.linalg.norm(np.array([[2,3], [X,Y]])))   \
    0.39 * phi(np.linalg.norm(np.array([[4,2], [X,Y]])))

surf = ax.plot_surface(X, Y, Z, cmap='viridis')

plt.xlim(0, 6)
plt.ylim(0, 6)
plt.show()

Something seems to be wrong with the parameter that I pass to the phi()-function but I'm not sure what it is. So how can I calculate the Z value correctly?

Note: I found a similar

CodePudding user response：

As @Mateo Vial mentioned in the comments, the simplest approach is to calculate the norm with the pythagorean formula. The working code looks like this:

import numpy as np
import matplotlib.pyplot as plt 

def phi(x):
    return np.exp(- np.power(x, 2))

fig = plt.figure(figsize=(8,7))
ax = fig.add_subplot(projection='3d')

x = np.arange(0, 6, 0.25)
y = np.arange(0, 6, 0.25)
X, Y = np.meshgrid(x, y)

Z = 0.49 * phi(np.sqrt((1-X)**2 (1-Y)**2))   \
    0.79 * phi(np.sqrt((2-X)**2 (3-Y)**2))   \
    0.39 * phi(np.sqrt((4-X)**2 (2-Y)**2))

surf = ax.plot_surface(X, Y, Z, cmap='viridis')

plt.xlim(0, 6)
plt.ylim(0, 6)
plt.show()

And now the result is a good interpolation with a radial basis function.