Out of an array of arbitrary unit vectors, what is the most efficient method of finding the two vect-CodePudding

So I'm attempting to make a wall system like the Sims. While it is 3D, it can be simplified to 2D (think a bird's eye view). A wall is defined by two points: a starting point an an ending point and the walls themselves have directions and can be simplified to unit vectors. Walls are also made with rectangular prisms, each of these prisms start at one point and end at another. So, bearing this in mind, sometimes walls have to be extended, otherwise there will be a small gap in the convex corner of the wall

if one of the points is shared between the walls. Any number of walls can be placed in a single position, so all of this in mind, a grid point's data could contain something like this (using Lua), each table represents a vector2, using a table for ease of visualization, this code won't actually work:

local gridPoint = {
  {x = 1, y = 0},
  {x = 0.7071, y = 0.7071},
  {x = 0, y = 1},
  {x = 0.7071, y = -0.7071},
}

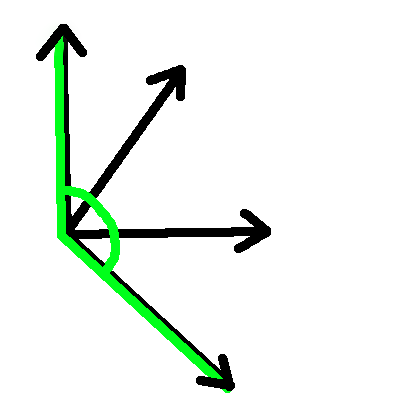
Here's a visual of what the points might look like, where the intersection is the grid point and the walls are the vectors extending from the intersection, assuming each of the vectors have a length of 1 (excuse my terrible drawing skills). Since dot products flip when greater than 180 degrees, the largest angle would always be <=180.

So now, to get the angle between any two of points, we can just do math.deg(math.acos(v1:dot(v2))) to get the angle between these two points in degrees, where v1 is vector 1, v2 is vector 2, and dot is a function that returns the dot product of v1 and v2.

So up to this point, everything is fine. The issue is that I have to create two loops which goes through every single combination of possible dot products which I'm not sure is the best method of finding the largest angle, this is #gridPoint^2 possible combinations which is fine at lower numbers, but this number of possible combination increases exponentially with each new wall.

Is there an easier way of doing this?

CodePudding user response：

This problem is equivalent to finding of the farthest pair of points, where all the points lie at unit circle.

Sort points - it is simpler to separate points with positive y (angles 0..Pi) into the first list, and points with negative y into the second list,sort them by X-coordinate, then join the first list and reversed second one. This stage takes O(nlogn) time

Then perform searching of the farthest points - fix the first point index (A[i]), walk through the list until squared distance A[i]-A[j 1] becomes less than squared distance A[i]-A[j]. So we find the farthest point A[j] for A[i]. Now increment i and search the farthest point for it - starting from j.
Repeat until j exceeds n.

This stage is linear because we move i and j only in forward direction. Essentially this is a method of rotating calipers, so you can get some implementation elsewhere.