way for multiplication of these tensors with gradients-CodePudding

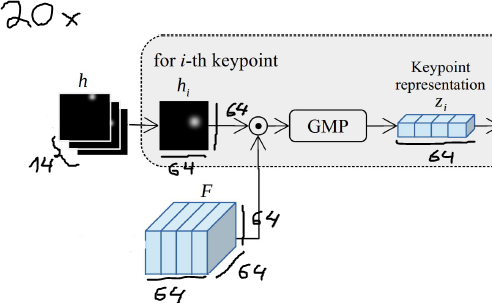
I have a function with two inputs: heat maps and feature maps. The heatmaps have a shape of (20, 14, 64, 64) and the feature maps have a shape of (20, 64, 64, 64). Where 20 is the batch size and 14 is the number of key points. Both heatmaps and feature maps have spatial dimensions of 64x64 and the featuremaps have 64 channels (on the second dimension).

Now I need to multiply each heatmap by each channel of the feature maps. So the first heatmap has to be multiplied by all 64 channels of the feature maps. The second with all channels, and so on.

After that, I should have a tensor of shape (20, 14, 64, 64, 64) on which I need to apply global max-pooling.

The problem is now that I can't create a new tensor to do that, because the gradients of the heatmaps and feature maps must be preserved.

My actual (slow and not-gradient-keeping) code is:

def get_keypoint_representation(self, heatmaps, features):
    heatmaps = heatmaps[0]
    pool = torch.nn.MaxPool2d(features.shape[2])
    features = features[:, None, :, :, :]
    features = features.expand(-1, 14, -1, -1, -1).clone()

    for i in range(self.cfg.SINGLE_GPU_BATCH_SIZE):
        for j in range(self.cfg.NUM_JOINTS):
            for k in range(features.shape[2]):
                features[i][j][k] = torch.matmul(heatmaps[i][j], features[i][j][k])

    gmp = features.amax(dim=(-1, -2))
    return gmp

Overview of the task:

CodePudding user response：

Given a tensor of heatmaps hm shaped (b, k, h, w) and a feature tensor fm shaped (b, c, h, w).

You can perform such an operation with a single einsum operator

>>> z = torch.einsum('bkhw,bchw->bkchw', hm, FM)
>>> z.shape
torch.Size([20, 14, 64, 64, 64])

Then follow with a max-pooling operation over the spatial dimensions using amax:

 >>> gmp = z.amax(dim=(-1,-2))
 >>> gmp.shape
 torch.Size([20, 14, 64])