What is the best algorithm to get maximum total value in binary tree?-CodePudding

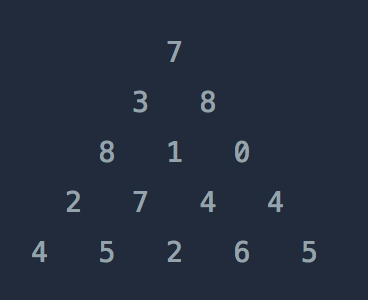
I have some questions about getting maximum sum value in binary tree.

Each node can have two child nodes (Left, Right)

Sum[7, 3, 8, 7, 5] is the maximum sum value for the example above.

First, I thought choosing each max child node is best answer, but it is not.

triangle = [[7], [3, 8], [8, 1, 0], [2, 7, 4, 4], [4, 5, 2, 6, 5]]
depth = 0
total = []

N = triangle[0][0]

def min_max(depth, N, total):
    if (depth 1) == len(triangle):
        return total
    else:
        a,b = triangle[depth 1][triangle[depth].index(N)], triangle[depth 1][triangle[depth].index(N) 1]
        total.append(max(a,b))
        N = max(a,b)
        return min_max(depth 1, N, total)

min_max(depth, N, total) # [8, 1, 7, 5]

Then, I thought getting all cases sum and comparing, but it seems to worsen the time complexity.

What is the proper algorithm for this task?

CodePudding user response：

I'm guessing you want the maximum sum of a path from the root of the tree to any child. With a minimax algorithm, you can acheive a time complexity of roughly O(2^N), where N is the depth of the tree.

However, I have here an O(N^2) dynamic programming solution to your problem, where N is the depth of the tree, and therefore O(N^2) is the scale of the number of nodes in the tree.

Define dp[i] to be the maximum sum of a path from the root of the tree to node i. Your base case is dp[root] = value of the root node. Iterate through the nodes from top to bottom (so root to child), and the dp function is

dp[node] = value_of_node[node] max(dp[top_left_of[node]], dp[top_right_of[node]]);

Hopefully this is intuitive: the maximum sum of a path to a certain node has to come from either its top left or top right node.

Your answer is the maximum of all the dp values of the children of the tree.

CodePudding user response：

I'm not entirely sure what the issue is; a simple, recursive way to calculate the sum for a node's children should be enough.

def get_max(node):
    if not node:
        return 0
    return node.value   max(get_max(node.left), get_max(node.right))

Each node is visited only once, so this will have a complexity of O(number of nodes) = O(N)