Exponential fit in pandas-CodePudding

I have this data:

puf = pd.DataFrame({'id':[1,2,3,4,5,6,7,8],
                    'val':[850,1889,3289,6083,10349,17860,28180,41236]})

The data seems to follow an exponential curve. Let's see the plot:

puf.plot('id','val')

I want to fit an exponential curve ($$ y = Ae^{Bx} $$, A times e to the B*X)and add it as a column in Pandas. Firstly I tried to log the values:

puf['log_val'] = np.log(puf['val'])

And then to use Numpy to fit the equation:

puf['fit'] = np.polyfit(puf['id'],puf['log_val'],1)

But I get an error:

ValueError: Length of values (2) does not match length of index (8)

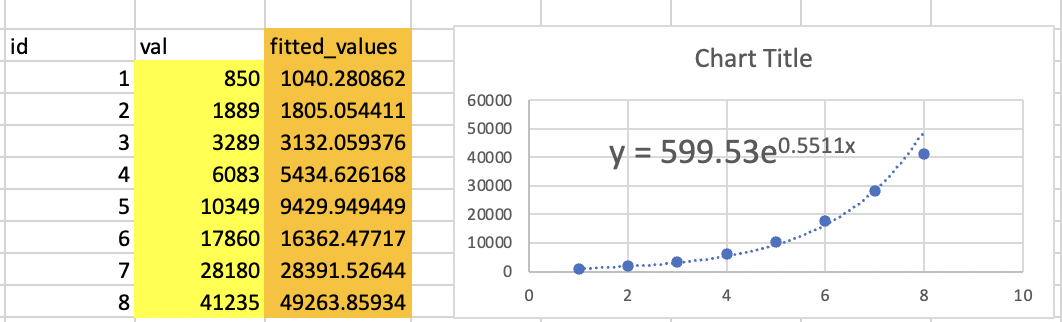
My expected result is the fitted values as a new column in Pandas. I attach an image with the column fitted values I want (in orange):

I'm stuck in this code. I'm not sure what I am doing wrong. How can I create a new column with my fitted values?

CodePudding user response：

Your getting that error because np.polyfit(puf['id'],puf['log_val'],1) returns two values array([0.55110679, 6.39614819]) which isn't the shape of your dataframe.

This is what you want

y = a* exp (b*x) -> ln(y)=ln(a) bx
f = np.polyfit(df['id'], np.log(df['val']), 1)

where

a = np.exp(f[1]) -> 599.5313046712091
b = f[0] -> 0.5511067934637022

Giving

puf['fit'] = a * np.exp(b * puf['id'])

   id    val           fit
0   1    850   1040.290193
1   2   1889   1805.082864
2   3   3289   3132.130026
3   4   6083   5434.785677
4   5  10349   9430.290286
5   6  17860  16363.179739
6   7  28180  28392.938399
7   8  41236  49266.644002

CodePudding user response：

Note that you asked for an exponential model yet you have the results for log-linear model.

Check out the work below:

For log-linear, we are fitting E(log(Y))ie log(y) - (log(b[0]) b[1]*x):

from scipy.optimize import least_squares
least_squares(lambda b: np.log(puf['val']) -(np.log(b[0])   b[1] * puf['id']), 
        [1,1])['x']
 array([5.99531305e 02, 5.51106793e-01])

These are the values that excel gives.

On the other hand to fit an exponential curve, the randomness is on Y and not on its logarithm, E(Y)=b[0]*exp(b[1] *x) Hence we have:

least_squares(lambda b: puf['val'] - b[0]*exp(b[1] * puf['id']), [0,1])['x']
array([1.08047304e 03, 4.58116127e-01]) # correct results for exponential fit

Depending on your model choice, the values are alittle different.

Better Model? Since you have same number of parameters, consider the one that gives you lower deviance or better out of sample prediction

Note that the ideal exponential model is E(Y) = A'B'^X which for comparison can be written as log(E(Y)) = A XB while log-linear model will be E(log(Y) = A XB. Note the difference in Expectation