How to shade area under the intersection of two distribution plots in matplotlib?-CodePudding

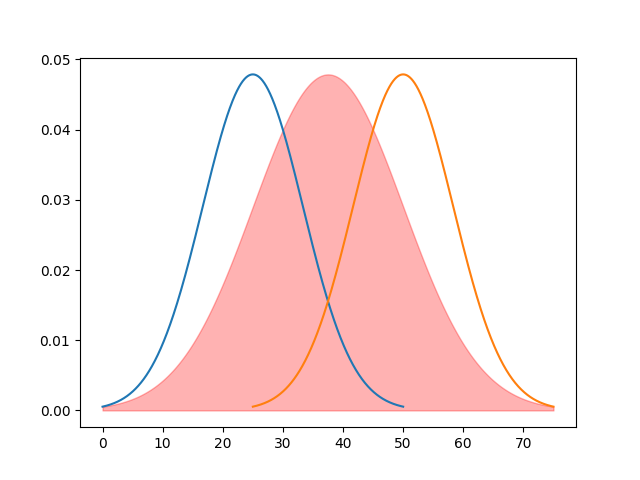
I'm trying to shade the area under the intersection of two distributions. I have this code so far, but I can't seem to figure out how to shade just the intersection with fill_between. How do I do this?

import matplotlib.pyplot as plt
import numpy as np
import scipy.stats as stats

p1_mu = 25
p2_mu = 50
p1_sigma = 25/3
p2_sigma = p1_sigma

p1 = np.linspace(p1_mu - 3 * p1_sigma, p1_mu   3 * p1_sigma, 1000)
p2 = np.linspace(p2_mu - 3 * p2_sigma, p2_mu   3 * p2_sigma, 1000)

p1_pdf = stats.norm.pdf(p1, p1_mu, p1_sigma)
p2_pdf = stats.norm.pdf(p2, p2_mu, p2_sigma)

xmin = min(min(p1), min(p2))
xmax = max(max(p1), max(p2))
x = np.linspace(xmin, xmax, 1000)
y = np.minimum(p2_pdf, p1_pdf)

fig, ax = plt.subplots()

ax.plot(p1, p1_pdf)
ax.plot(p2, p2_pdf)
ax.fill_between(x, y, color='red', alpha=0.3)
plt.show()

CodePudding user response：

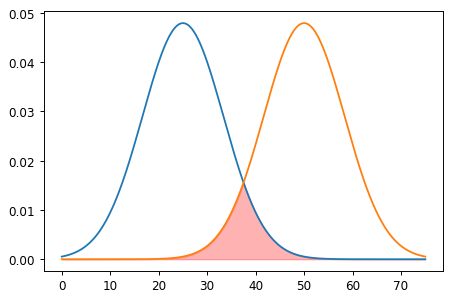
In your example both distributions are evaluated over a different range (p1 and p2). So the elements in p1_pdf & p2_pdf aren't aligned, in terms of the x-coordinates.

If you evaluate them the same, taking the minimum of both would work to get the intersection.

import matplotlib.pyplot as plt
import numpy as np
import scipy.stats as stats

p1_mu = 25
p2_mu = 50
p1_sigma = 25/3
p2_sigma = p1_sigma

# share x-range to evaluate on
pn = np.linspace(
    min(p1_mu-3*p1_sigma, p2_mu-3*p2_sigma), 
    max(p1_mu 3*p1_sigma, p2_mu 3*p2_sigma), 
    1000
)

p1_pdf = stats.norm.pdf(pn, p1_mu, p1_sigma)
p2_pdf = stats.norm.pdf(pn, p2_mu, p2_sigma)
y = np.minimum(p1_pdf, p2_pdf)

fig, ax = plt.subplots(dpi=86, facecolor="w")

ax.plot(pn, p1_pdf)
ax.plot(pn, p2_pdf)
ax.fill_between(pn, y, color='red', alpha=0.3)

The 1000 points at which to evaluate are now more spread, they cover a larger range, so if things like resolution are very important you might want to adjust that. And you can of course still create the p1_pdf & p2_pdf using their own range as in your OP, I just combined them for convenience.