Is point inside a circle sector-CodePudding

I need help on how to determine if a point "D" is inside a circle sector of 180°, known radius & center "B". As for the direction of the sector I don't know how to explain it with words so I made a sketch but basically it depends on another point "A".

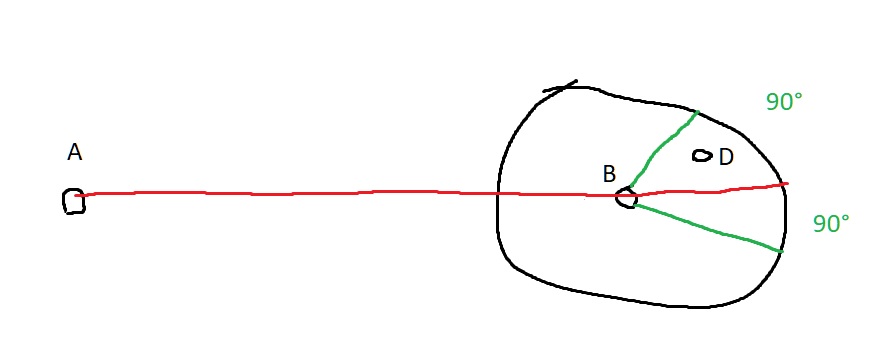
sketch

An explanation would be good enough but I'm not very good at maths so if you could give me a pseudocode it would be perfect!

Thanks !

CodePudding user response：

What you are looking for is the angle ψ below, to test if it is within certain limits (like /- 90°)

fig1

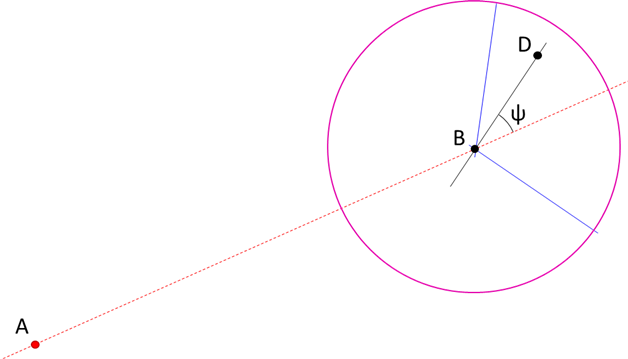
This can be done by finding the angle ψ between the vectors B-A and D-B.

The angle between them is found using the following dot and cross product rules

fig2 fig3

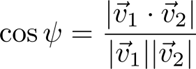
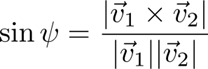
and the pseudocode using the atan2(dy,dx) function that must programming environments have

v_1.x = B.x-A.x
v_1.y = B.y-A.y
v_2.x = D.x-B.x
v_2.y = D.y-B.y

ψ = atan2( (v_1.x*v_2.y - v_1.y*v_2.x), (v_1.x*v_2.x   v_1.y*v_2.y) )

Note that the result is within -π and π covering all 4 quadrants

Now just check if abs(ψ) <= π/2.

_{Take a note of the definition of atan2 since some environments define it as atan2(dx,dy) and some as atan2(dy,dx), where the angle is measured such that dx=r*cos(ψ) and dy=r*sin(ψ).}