Signed int not being converted into unsigned int-CodePudding

I am reading the book C Primer, by Lippman and Lajoie. On page 65 they say: If we use both unsigned and int values in an arithmetic expression, the int value ordinarily is converted to unsigned.

If I try out their example, things work as expected, that is:

unsigned u = 10;
int i = -42;
std::cout << u   i << std::endl; // if 32-bit ints, prints 4294967264

However, if I change i to -10, the result I get is 0 instead of the expected 4294967296, with 32-bit ints:

unsigned u = 10;
int i = -10;
std::cout << u   i << std::endl; // prins 0 instead of 4294967296. Why?

Shouldn't this expression print 10 (-10 mod 2^32) ?

CodePudding user response：

Both unsigned int and int take up 32 bits in the memory, let's consider their bit representations:

unsigned int u = 10;
00000000000000000000000000001010

int i = -42;
11111111111111111111111111010110

u   i:
11111111111111111111111111100000

If we treat 11111111111111111111111111100000 as a signed number (int), then it is -32:

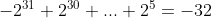
If we treat it as an unsigned number (unsigned), then it is 4294967264:

The difference lies in the highest bit, whether it represents -2^31, or 2^31.

Now let's take a look at (10u) (-10):

   unsigned int u = 10;
   00000000000000000000000000001010

   int i = -10;
   11111111111111111111111111110110

   u   i:
(1)00000000000000000000000000000000

Since u i will be over 32 bits limit, the highest bit 1 will be discarded. Since the remaining 32 bits are all zero, the result will be 0. Similarly, if i = -9, then the result will be 1.