Question here:
Given a polygon P, a circle C_init, and a direction D, let C_init move along D, it might have collision with P (C_target below). How to calculate the distance between C_init and C_target?
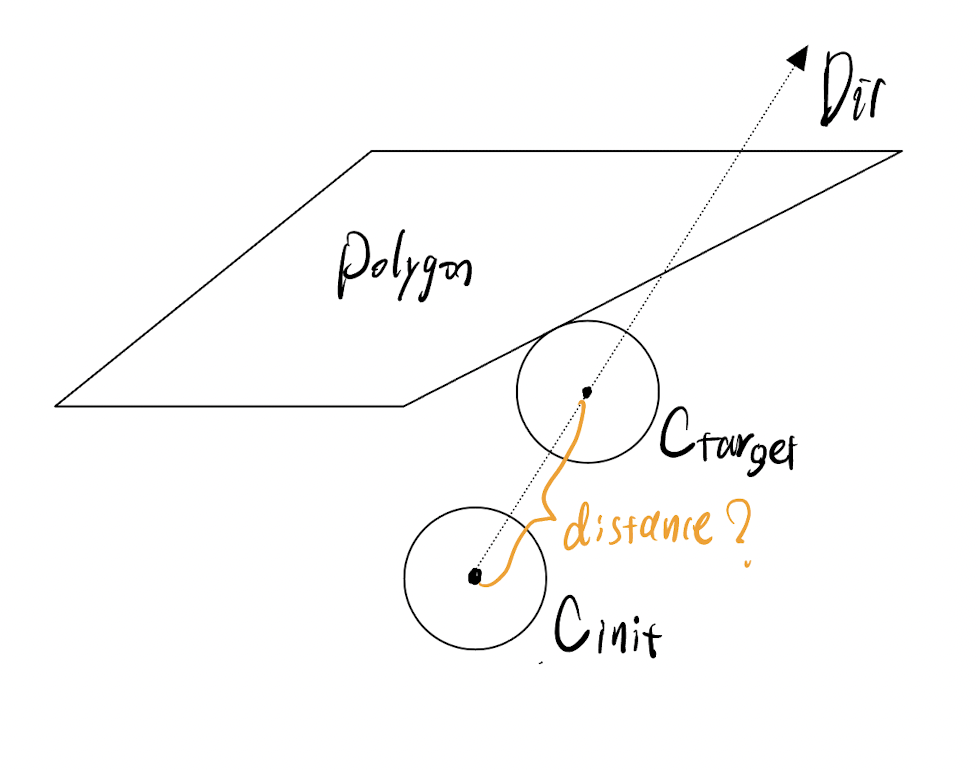
Any help is appreciated!
CodePudding user response:
Given that computing the perpendicular distance between a point and a line is a well hashed-out problem, do the following:
- Find a parametrization of the line along which you're moving
- Solve for the value of the parameter that gives you a distance R to each line of the polygon
- Select the first solution that lies within the line segment of the corresponding polygon side.
- Convert the parameter to distance on the line.
CodePudding user response:
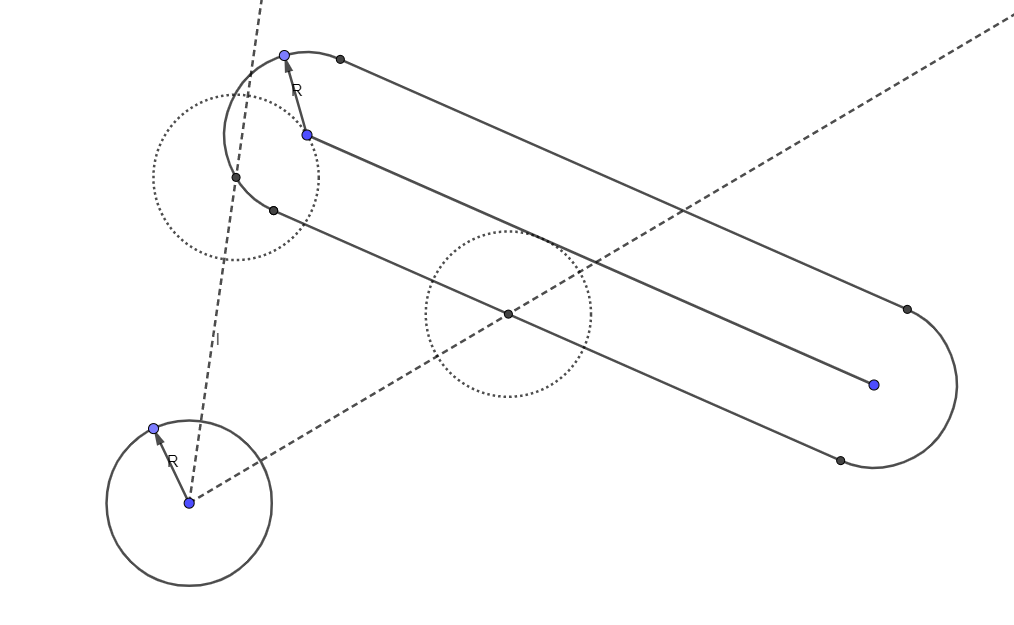
When the circle collides with the line segment, the centre of the circle lies on the offset segment (the lozenge shape around the segment).
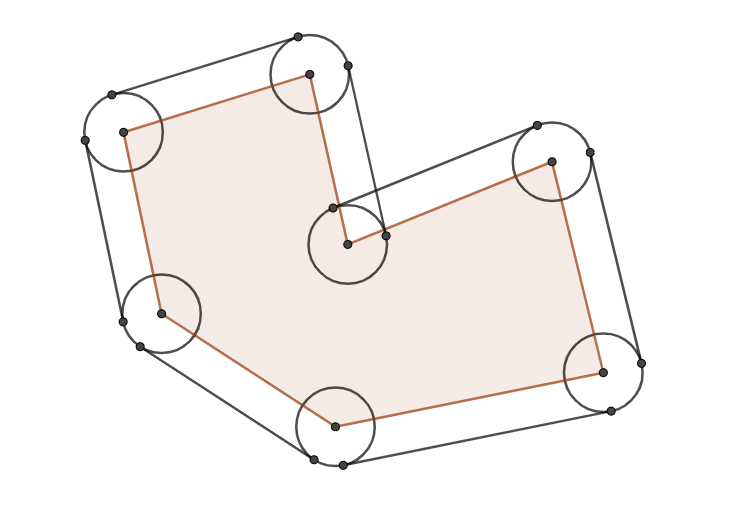
One easy way to compute the intersection is to place a circle of radius R at each vertex of the polygon, offset each edge outwards by R, and intersect the ray shooting from the centre of your moving circle with each of the new circles and offset edges. The closest intersection point would be your collision point.
As the picture shows, there is no need to place a circle at reflex angles (>2π) of the polygon as the circle can never collide with such vertices.