I wanted to know if the algorithm that i wrotte just below in python is correct.

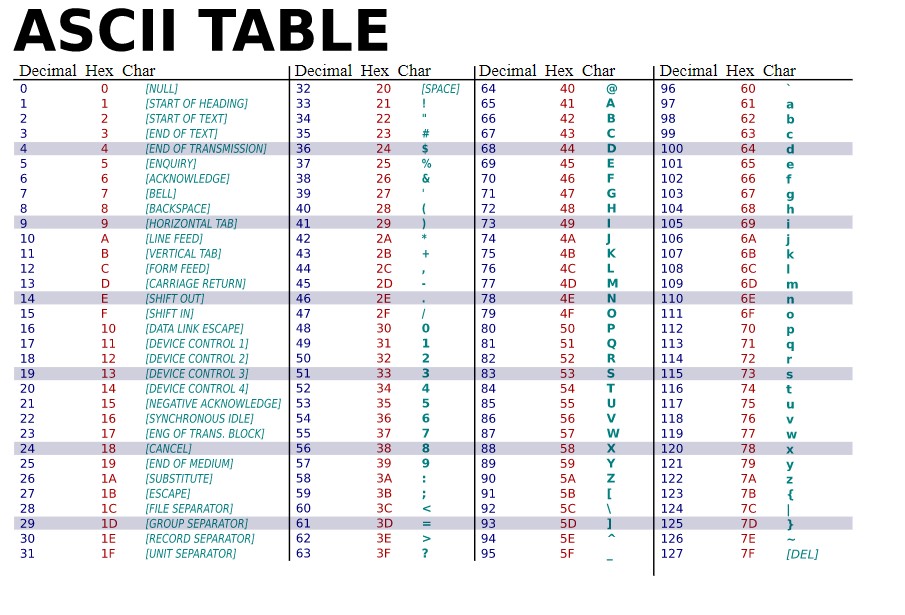
My goal is to find an algorithm that print/find all the possible combinaison of words that can be done using the character from character '!' (decimal value = 33) to character '~' (decimal value = 126) in the asccii table:

Here the code using recursion:

byteWord = bytearray(b'\x20')  # Hex = '\x21' & Dec = '33' & Char = '!'

cntVerif = 0  # Test-------------------------------------------------------------------------------------------------------


def comb_fct(bytes_arr, cnt: int):
    global cntVerif  # Test------------------------------------------------------------------------------------------------

    if len(bytes_arr) > 3:  # Test-----------------------------------------------------------------------------------------
        print(f'{cntVerif 1}:TEST END')
        sys.exit()

    if bytes_arr[cnt] == 126:
        if cnt == len(bytes_arr) or len(bytes_arr) == 1:
            bytes_arr.insert(0, 32)
        bytes_arr[cnt] = 32
        cnt  = 1
        cntVerif  = 1  # Test----------------------------------------------------------------------------------------------
        print(f'{cntVerif}:if bytes_arr[cnt] == 126: \n\tbytes_arr = {bytes_arr}')  # Test-------------------------------------------------------------------------------------------
        comb_fct(bytes_arr, cnt)

    if cnt == -1 or cnt == len(bytes_arr)-1:
        bytes_arr[cnt] = bytes_arr[cnt]   1
        cntVerif  = 1  # Test----------------------------------------------------------------------------------------------
        print(f'{cntVerif}:if cnt==-1: \n\tbytes_arr = {bytes_arr}')  # Test-------------------------------------------------------------------------------------------
        comb_fct(bytes_arr, cnt=-1)  # index = -1 means last index

    bytes_arr[cnt] = bytes_arr[cnt]   1
    cntVerif  = 1  # Test--------------------------------------------------------------------------------------------------
    print(f'{cntVerif}:None if: \n\tbytes_arr={bytes_arr}')  # Test-----------------------------------------------------------------------------------------------
    comb_fct(bytes_arr, cnt 1)


comb_fct(byteWord, -1)

Thank your for your help because python allow just a limited number of recursion (996 on my computer) so i for exemple i can't verify if my algorithm give all the word of length 3 that can be realised with the range of character describe upper.

Of course if anyone has a better idea to writte this algorithm (a faster algorithm for exemple). I will be happy to read it.

CodePudding user response：

You don't need a recursion here. Consider your word as a n-digit number, where the digits are ASCII symbols in the range of interest ([!..~]). Start with the smallest one (all !), and increment it by 1, until you reach the largest (all ~).

To increment the long number, add 1 to the least significant byte. If it becomes ~, make it ! and try to increment the next one, etc.

Keep in mind that the amount of words is huge. There are 94 ** n n-letter words. For n == 4 there are 78074896 of them.

CodePudding user response：

To solve this problem i think that i ve found an elegant and faster way to do it without using recursive algorithm. I think too that it is the time optimal solution (as it is O(n))
I am using the fact that it exists a bijection between all the number in decimal basis and the number in base 94.
It is obvious that each number in base 94 can be written using a special sequance of unique character as the one in the range [30, 126] (in decimal value) in the ascii code.

I will be happy if anyone can confirm that my solution is correct. :-)

# Get all ascii relevant character in a list
asciiList = []
for c in (chr(i) for i in range(33, 127)):
    asciiList.append(c)
print(f'ascii List: \n{asciiList} \nlist length: {len(asciiList)}')


def base10_to_base94_fct(int_to_convert: int) -> str:
    sol_str = ''
    loop_condition = True

    while loop_condition is True:
        quo = int_to_convert // 94
        mod = int_to_convert % 94
        sol_str = asciiList[mod]   sol_str
        int_to_convert = quo
        if quo == 0:
            loop_condition = False

    return sol_str


# test = base10_to_base94_fct(94**2-1)
# print(f'TEST result: {test}')


def comb_fct(word_length: int) -> None:
    max_iter = 94**word_length

    cnt = 1
    while cnt < max_iter:
        str_tmp = base10_to_base94_fct(cnt)
        cnt  = 1
        print(f'{cnt}: Current word check:{str_tmp}')


# Test
comb_fct(3)

exemple of base conversion:
https://www.rapidtables.com/convert/number/decimal-to-hex.html
The operator '//' is the quotient operator and the operator '%' is the modulo operator.