Javascript math recursive function optimisation-CodePudding

This is what I've got

let base = 10000
let yearly = 31557600
let apy = 0.09

let loop = 0;
let new_base = '0';
function recurse(base){
    new_base = base*(1 apy*1/(yearly));
    if(loop < 3600){
        loop  ;
        return recurse(new_base);    
    }
    else {
        return new_base;
    }
}
base = recurse(base);
console.log(base);

if I change 3600 by a very large number I get the error: Maximum call stack size exceeded

This seems normal to me because the recursive operation is executed too many times,

what would be the solution ? Is it possible to transform the recursive function into a linear function for example?

Thanks

CodePudding user response：

Well it can be transformed to an equation, but not a linear one.

Here, is the approach:

I will rename the base as b0, and the new base as b1

b1 = b0 * (1 (apy/yearly)

and after loop is incremented new base will be updated, let's call the new b1 as b2:

b2 = b1 * (1 (apy/yearly))

b2 = b0 * (1 (apy/yearly))^2

and so on..

so the final returned value will be:

base * (1 (apy/yearly))^3600

and the general formula will be

base * (1 (apy/yearly))^n, where n is 3600 in your case.

Putting the constants plugged in you will get 10,000.102669931423184360664719158

Please remember to upvote this answer if it solves your problem.

CodePudding user response：

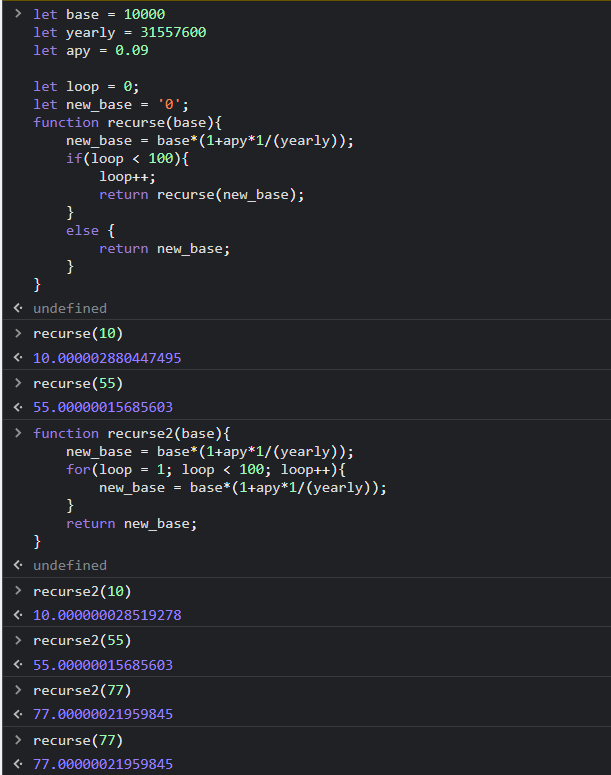
Do you need recursion? No.

function recurse2(base){
    new_base = base*(1 apy*1/(yearly));
    for(loop = 1; loop < 100; loop  ){
        new_base = base*(1 apy*1/(yearly));
    }
    return new_base;
}

You don't even tail optimization. This is just a value that is being mutated over and over. You don't need a new stackframe (function call) to mutate said value, just loop over it.

How did I arrive at this function? Just think what happens to the base when you pass it in and how it changes with each "recursion". It just gets multiplied by some expression each time. So we can just do that in a loop.

You can even improve the code snippet that I have here with a do {} while();

The following screenshot shows quick tests that show that function recurse2 that I wrote is identical*.