Running multiply Anova and/or T-Test on variables in one dataframe in R-CodePudding

I've the a data frame containing different items (and it's cost) and also it's subsequent groupings. I would like to run an Anova and/or T-Test for each item based on their groupings to see if their mean differs. Anybody knows how to do this in R?

A sample of the dataframe is as follow:

Item	Cost	Grouping
Book A	7	A
Book A	9	B
Book A	6	A
Book A	7	B
Book B	4	A
Book B	6	B
Book B	5	A
Book B	3	C
Book C	5	C
Book C	4	A
Book C	7	C
Book C	2	B
Book C	2	B
Book D	4	A
Book D	2	C
Book D	9	C
Book D	4	A

The output should be a simple table (or any similar table) as follows

Item	P-Value (from ANOVA/t-test) (H0: Mean same for all groupings)
Book A	xxx
Book B	xxx
Book C	xxx
Book D	xxx

Thanks in advance!

CodePudding user response：

Instead of dealing with multiple ANOVA, t-tests and worrisome (and potentially questionable) p-values, I would fit a single generalised linear mixed-effect model with group as a random effect. This is easy to do in a fully Bayesian way using rstanarm, which gives full posterior distributions for the means of every item. Instead of worrying about the suitability & interpretability of (multiple) hypothesis tests, we can then compare posterior distributions for the means directly.

library(rstanarm)
model <- stan_glmer(cost ~ 0   item   (1 | group), data = df)

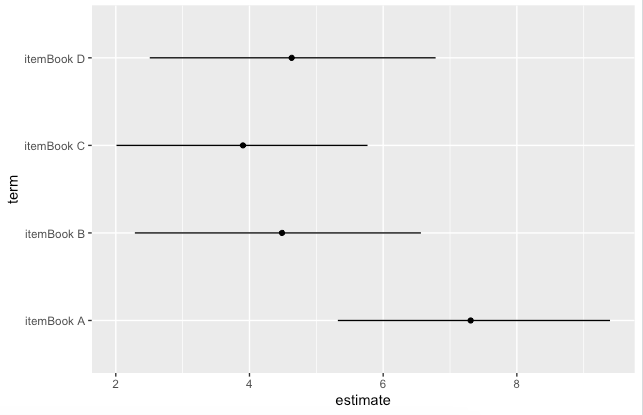
We can summarise the mean posterior distributions by showing the posterior median and 90% posterior uncertainty intervals per item.

library(broom.mixed)
tidy(model, conf.int = TRUE) %>%
    ggplot(aes(y = term))   
    geom_point(aes(x = estimate))   
    geom_linerange(aes(xmin = conf.low, xmax = conf.high))

Or as a table

tidy(mode, conf.int = TRUE)
## A tibble: 4 × 5
#  term       estimate std.error conf.low conf.high
#  <chr>         <dbl>     <dbl>    <dbl>     <dbl>
#1 itemBook A     7.28      1.17     5.09      9.40
#2 itemBook B     4.44      1.16     2.27      6.45
#3 itemBook C     3.88      1.05     1.89      5.75
#4 itemBook D     4.63      1.21     2.41      6.71

Here,

estimate is the posterior median,
std.error is the posterior MAD, and
conf.low and conf.high are the lower and upper bounds of the 90% posterior uncertainty interval.

CodePudding user response：

You could use anova_test from the rstatix package like this:

df <- data.frame(Item = c("Book A", "Book A", "Book A", "Book A", "Book B", "Book B", "Book B", "Book B"),
                 Cost = c(7,9,6,7,4,6,5,3),
                 Grouping = c("A", "B", "A", "B", "A", "B", "A", "C"))

library(dplyr)
library(rstatix)
df %>% 
  group_by(Item) %>%
  anova_test(Cost ~ Grouping)
#> Coefficient covariances computed by hccm()
#> Coefficient covariances computed by hccm()
#> # A tibble: 2 × 8
#>   Item   Effect     DFn   DFd     F     p `p<.05`   ges
#> * <chr>  <chr>    <dbl> <dbl> <dbl> <dbl> <chr>   <dbl>
#> 1 Book A Grouping     1     2   1.8 0.312 ""      0.474
#> 2 Book B Grouping     2     1   4.5 0.316 ""      0.9

^{Created on 2022-07-10 by the reprex package (v2.0.1)}