How to recover the amplitude of array after doing Numpy Gradient?-CodePudding

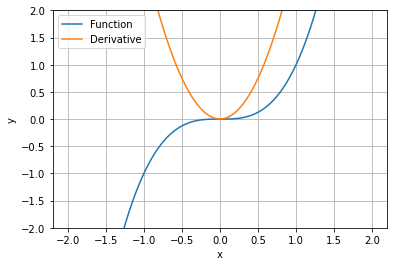
I have the function y=x^3 and its derivative dy = 3*x^2. Using numeric vectors, I do:

x, sp = np.linspace(-3,3,100, retstep=True)
y = x**3
dy = np.gradient(y, sp)

plt.figure(figsize=(6,4))
plt.plot(x,y1,label='Function')
plt.plot(x,y2,label='Derivative')
plt.xlabel('x')
plt.ylabel('y')
plt.ylim(-2,2)
plt.legend()
plt.grid()
plt.show()

You can clearly see that the derivative is wrong because the curves should intersect themselves in (1,1). How do I calculate the derivative with the proper amplitude?

CodePudding user response：

Derivative of x**3 is 3*x². At point x=1, your function is 1 because 1**3 = 1.
The derivative at x=1 is 3*1²=3. Why would they intersect at (1,1) when the derivative is (1,3)?