I am a beginner, and i have this fundamental doubt...
What is the Big-O runtime of this simple algorithm ?
Is it O(n²) [ cause of two for loops ] or O(n³) [ including product of two numbers which itself should be O(n) ] ?

MaxPairwiseProductNaive(A[1 . . . n]):
product ← 0
for i from 1 to n:
for j from i   1 to n:
product ← max(product, A[i] · A[j])
return product

CodePudding user response：

Both your first and second loops are O(n), so together they are O(n^2).

Inside your loop, neither the max or multiplication depend on the number of array elements. For languages like C, C , C#, Java, etc., getting a value from an array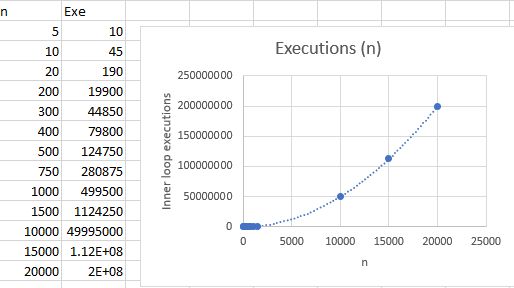

That trendline is just barely under executions = 0.5n^2. Which makes sense if you think about low numbers of n. You can step through your loops on a piece of paper and immediately see the pattern.

• n=5: 5 outer loop iterations, 10 total inner loop iterations
• n=10 10 outer loop iterations, 45 total inner loop iterations
• n=20 20 outer loop iterations, 190 total inner loop iterations

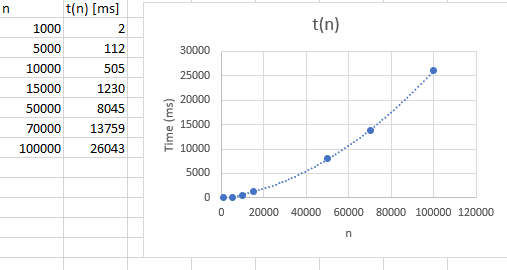
For timing, we see an almost identical trend with just a different constant. This indicates that our time, T(n), is directly proportional to the number of inner loop iterations.

Takeaway:

The analysis which gave O(n^2) worked perfectly. The statements within the loop were O(1) as expected. The check didn't end up being necessary, but it's useful to see just how closely the analysis and verification match.