Consider the following code:
BigInteger value = BigInteger.Parse("9876543210987654321098765432109876543210");
Console.WriteLine(value.ToString().Length); // 40
Is there a more efficient way to get the length of the number without calling ToString?
CodePudding user response:
Anytime a question asks about "performance", it is always necessary to benchmark the approaches. As madreflection pointed out, there is both cpu and memory costs to consider, so I ran benchmarks targeting .NET 6 with a memory diagnoser. The results are fascinating and Joel's answer performs very poorly compared to the highly optimized ToString() and Log10 methods of BigInteger.
Benchmark Code:
[SimpleJob(RuntimeMoniker.Net60)]
[MemoryDiagnoser]
public class BigIntegerBenchmarks
{
private static BigInteger _value = BigInteger.Parse("9876543210987654321098765432109876543210");
[Benchmark(Baseline = true)]
public int ToStringBenchmark()
{
return _value.ToString().Length;
}
[Benchmark]
public int GetLengthDivisionBenchmark()
{
return GetLengthDivision(_value);
}
[Benchmark]
public int GetLengthMultiplicationBenchmark()
{
return GetLengthMultiplication(_value);
}
[Benchmark]
public int GetLengthAbsPowBenchmark()
{
return GetLengthAbsPow(_value);
}
[Benchmark]
public int BigIntegerLog()
{
return (int)Math.Round(BigInteger.Log10(_value), MidpointRounding.AwayFromZero);
}
[Benchmark]
public int CountDigitsBenchmark()
{
return CountDigits(_value);
}
static int GetLengthDivision(BigInteger value)
{
int result = 1;
while (value >= 10)
{
result ;
value /= 10;
}
return result;
}
static int GetLengthMultiplication(BigInteger value)
{
BigInteger power = 10;
int result = 1;
while (power < value)
{
result ;
power *= 10;
}
return result;
}
static int GetLengthAbsPow(BigInteger value)
{
int result = 1;
BigInteger ten = new(10);
BigInteger absValue = BigInteger.Abs(value);
while (BigInteger.Pow(ten, result) < absValue)
{
result ;
}
return result;
}
internal static int CountDigits(BigInteger value)
{
int num = 1;
BigInteger num2;
if (value >= 10000000)
{
if (value >= 100000000000000L)
{
num2 = value / 100000000000000;
num = 14;
while (num2 >= 10)
{
num ;
num2 /= 10;
}
}
else
{
num2 = value / 10000000;
num = 7;
}
}
else
{
num2 = (uint)value;
}
if (num2 >= 10)
{
num = ((num2 < 100) ? (num 1) : ((num2 < 1000) ? (num 2) : ((num2 < 10000) ? (num 3) : ((num2 < 100000) ? (num 4) : ((num2 >= 1000000) ? (num 6) : (num 5))))));
}
return num;
}
}
Results:
BenchmarkDotNet=v0.13.1, OS=Windows 10.0.19043.1826 (21H1/May2021Update)
Intel Core i7-8565U CPU 1.80GHz (Whiskey Lake), 1 CPU, 8 logical and 4 physical cores
.NET SDK=7.0.100-preview.4.22252.9
[Host] : .NET Core 3.1.24 (CoreCLR 4.700.22.16002, CoreFX 4.700.22.17909), X64 RyuJIT
.NET 6.0 : .NET 6.0.5 (6.0.522.21309), X64 RyuJIT
Job=.NET 6.0 Runtime=.NET 6.0
| Method | Mean | Error | StdDev | Ratio | RatioSD | Gen 0 | Allocated |
|---|---|---|---|---|---|---|---|
| ToStringBenchmark | 160.96 ns | 3.200 ns | 2.837 ns | 1.00 | 0.00 | 0.0668 | 280 B |
| GetLengthDivisionBenchmark | 1,939.93 ns | 35.299 ns | 31.292 ns | 12.06 | 0.28 | 0.3052 | 1,288 B |
| GetLengthMultiplicationBenchmark | 1,330.02 ns | 21.522 ns | 20.131 ns | 8.26 | 0.17 | 0.5569 | 2,336 B |
| GetLengthAbsPowBenchmark | 10,928.05 ns | 123.547 ns | 115.566 ns | 67.89 | 1.25 | 3.4637 | 14,520 B |
| BigIntegerLog | 58.34 ns | 1.179 ns | 0.985 ns | 0.36 | 0.01 | - | - |
| CountDigitsBenchmark | 1,018.92 ns | 9.688 ns | 8.589 ns | 6.33 | 0.12 | 0.1774 | 744 B |
Notes:
- CountDigits is a clever method from System.Buffers.Text.FormattingHelpers that I adapted for BigInteger. It performs significantly better than Joel's methods, but far worse than either ToString or Log10.
- Matthew's adapted method was 5-10x worse than Joel's method, showing just how important benchmarking code can be when selecting an algorithm.
Conclusion:
BigInteger.Log10() seems to be by far the fastest method and causes zero memory allocations, although the need to round concerns me. You would have to determine if that rounding method is acceptable to you and worth the risk.
In addition, it is worth noting that the dotnet core team and open source community continue to heavily optimize the framework apis and runtime. It is critical to prove that they do in fact have a slow algorithm via benchmarking before rolling your own solution.
To Theodor Zoulias' point, the benchmarks against a single value are incomplete.
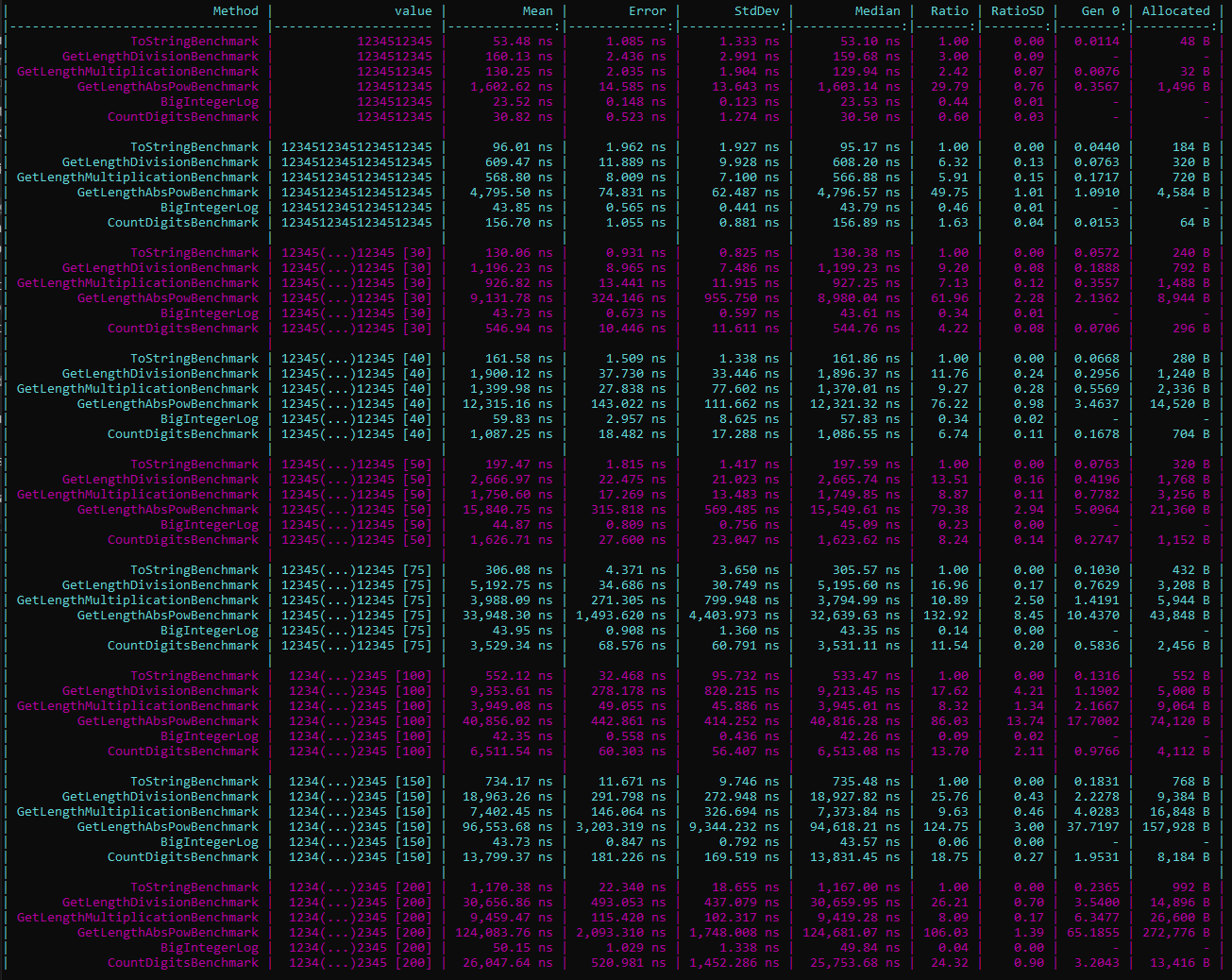
As a result, I ran additional benchmarks against BigInteger values ranging from 10 digits to 200 digits. In all cases, the winner was consistently the Log10 implementation. For very small numbers (10 digits) the CountDigits implementation beats ToString but not Log10.
Benchmark Code:
[SimpleJob(RuntimeMoniker.Net60)]
[MemoryDiagnoser]
public class BigIntegerBenchmarks
{
public IEnumerable<BigInteger> Values()
{
// 10
yield return BigInteger.Parse("1234512345");
// 20
yield return BigInteger.Parse("12345123451234512345");
// 30
yield return BigInteger.Parse("123451234512345123451234512345");
// 40
yield return BigInteger.Parse("1234512345123451234512345123451234512345");
// 50
yield return BigInteger.Parse("12345123451234512345123451234512345123451234512345");
// 75
yield return BigInteger.Parse("123451234512345123451234512345123451234512345123451234512345123451234512345");
// 100
yield return BigInteger.Parse("1234512345123451234512345123451234512345123451234512345123451234512345123451234512345123451234512345");
// 150
yield return BigInteger.Parse("123451234512345123451234512345123451234512345123451234512345123451234512345123451234512345123451234512345123451234512345123451234512345123451234512345");
// 200
yield return BigInteger.Parse("12345123451234512345123451234512345123451234512345123451234512345123451234512345123451234512345123451234512345123451234512345123451234512345123451234512345123451234512345123451234512345123451234512345");
}
[Benchmark(Baseline = true)]
[ArgumentsSource(nameof(Values))]
public int ToStringBenchmark(BigInteger value)
{
return value.ToString().Length;
}
[Benchmark]
[ArgumentsSource(nameof(Values))]
public int GetLengthDivisionBenchmark(BigInteger value)
{
return GetLengthDivision(value);
}
[Benchmark]
[ArgumentsSource(nameof(Values))]
public int GetLengthMultiplicationBenchmark(BigInteger value)
{
return GetLengthMultiplication(value);
}
[Benchmark]
[ArgumentsSource(nameof(Values))]
public int GetLengthAbsPowBenchmark(BigInteger value)
{
return GetLengthAbsPow(value);
}
[Benchmark]
[ArgumentsSource(nameof(Values))]
public int BigIntegerLog(BigInteger value)
{
return (int)Math.Floor(BigInteger.Log10(value) 1);
}
[Benchmark]
[ArgumentsSource(nameof(Values))]
public int CountDigitsBenchmark(BigInteger value)
{
return CountDigits(value);
}
static int GetLengthDivision(BigInteger value)
{
int result = 1;
while (value >= 10)
{
result ;
value /= 10;
}
return result;
}
static int GetLengthMultiplication(BigInteger value)
{
BigInteger power = 10;
int result = 1;
while (power < value)
{
result ;
power *= 10;
}
return result;
}
static int GetLengthAbsPow(BigInteger value)
{
int result = 1;
BigInteger ten = new(10);
BigInteger absValue = BigInteger.Abs(value);
while (BigInteger.Pow(ten, result) < absValue)
{
result ;
}
return result;
}
internal static int CountDigits(BigInteger value)
{
int num = 1;
BigInteger num2;
if (value >= 10000000)
{
if (value >= 100000000000000L)
{
num2 = value / 100000000000000;
num = 14;
while (num2 >= 10)
{
num ;
num2 /= 10;
}
}
else
{
num2 = value / 10000000;
num = 7;
}
}
else
{
num2 = (uint)value;
}
if (num2 >= 10)
{
num = ((num2 < 100) ? (num 1) : ((num2 < 1000) ? (num 2) : ((num2 < 10000) ? (num 3) : ((num2 < 100000) ? (num 4) : ((num2 >= 1000000) ? (num 6) : (num 5))))));
}
return num;
}
}
Results:
BenchmarkDotNet=v0.13.1, OS=Windows 10.0.19043.1826 (21H1/May2021Update)
Intel Core i7-8565U CPU 1.80GHz (Whiskey Lake), 1 CPU, 8 logical and 4 physical cores
.NET SDK=7.0.100-preview.4.22252.9
[Host] : .NET Core 3.1.24 (CoreCLR 4.700.22.16002, CoreFX 4.700.22.17909), X64 RyuJIT
.NET 6.0 : .NET 6.0.5 (6.0.522.21309), X64 RyuJIT
Job=.NET 6.0 Runtime=.NET 6.0
| Method | value | Mean | Error | StdDev | Median | Ratio | RatioSD | Gen 0 | Allocated |
|---|---|---|---|---|---|---|---|---|---|
| ToStringBenchmark | 1234512345 | 53.48 ns | 1.085 ns | 1.333 ns | 53.10 ns | 1.00 | 0.00 | 0.0114 | 48 B |
| GetLengthDivisionBenchmark | 1234512345 | 160.13 ns | 2.436 ns | 2.991 ns | 159.68 ns | 3.00 | 0.09 | - | - |
| GetLengthMultiplicationBenchmark | 1234512345 | 130.25 ns | 2.035 ns | 1.904 ns | 129.94 ns | 2.42 | 0.07 | 0.0076 | 32 B |
| GetLengthAbsPowBenchmark | 1234512345 | 1,602.62 ns | 14.585 ns | 13.643 ns | 1,603.14 ns | 29.79 | 0.76 | 0.3567 | 1,496 B |
| BigIntegerLog | 1234512345 | 23.52 ns | 0.148 ns | 0.123 ns | 23.53 ns | 0.44 | 0.01 | - | - |
| CountDigitsBenchmark | 1234512345 | 30.82 ns | 0.523 ns | 1.274 ns | 30.50 ns | 0.60 | 0.03 | - | - |
| ToStringBenchmark | 12345123451234512345 | 96.01 ns | 1.962 ns | 1.927 ns | 95.17 ns | 1.00 | 0.00 | 0.0440 | 184 B |
| GetLengthDivisionBenchmark | 12345123451234512345 | 609.47 ns | 11.889 ns | 9.928 ns | 608.20 ns | 6.32 | 0.13 | 0.0763 | 320 B |
| GetLengthMultiplicationBenchmark | 12345123451234512345 | 568.80 ns | 8.009 ns | 7.100 ns | 566.88 ns | 5.91 | 0.15 | 0.1717 | 720 B |
| GetLengthAbsPowBenchmark | 12345123451234512345 | 4,795.50 ns | 74.831 ns | 62.487 ns | 4,796.57 ns | 49.75 | 1.01 | 1.0910 | 4,584 B |
| BigIntegerLog | 12345123451234512345 | 43.85 ns | 0.565 ns | 0.441 ns | 43.79 ns | 0.46 | 0.01 | - | - |
| CountDigitsBenchmark | 12345123451234512345 | 156.70 ns | 1.055 ns | 0.881 ns | 156.89 ns | 1.63 | 0.04 | 0.0153 | 64 B |
| ToStringBenchmark | 12345(...)12345 [30] | 130.06 ns | 0.931 ns | 0.825 ns | 130.38 ns | 1.00 | 0.00 | 0.0572 | 240 B |
| GetLengthDivisionBenchmark | 12345(...)12345 [30] | 1,196.23 ns | 8.965 ns | 7.486 ns | 1,199.23 ns | 9.20 | 0.08 | 0.1888 | 792 B |
| GetLengthMultiplicationBenchmark | 12345(...)12345 [30] | 926.82 ns | 13.441 ns | 11.915 ns | 927.25 ns | 7.13 | 0.12 | 0.3557 | 1,488 B |
| GetLengthAbsPowBenchmark | 12345(...)12345 [30] | 9,131.78 ns | 324.146 ns | 955.750 ns | 8,980.04 ns | 61.96 | 2.28 | 2.1362 | 8,944 B |
| BigIntegerLog | 12345(...)12345 [30] | 43.73 ns | 0.673 ns | 0.597 ns | 43.61 ns | 0.34 | 0.01 | - | - |
| CountDigitsBenchmark | 12345(...)12345 [30] | 546.94 ns | 10.446 ns | 11.611 ns | 544.76 ns | 4.22 | 0.08 | 0.0706 | 296 B |
| ToStringBenchmark | 12345(...)12345 [40] | 161.58 ns | 1.509 ns | 1.338 ns | 161.86 ns | 1.00 | 0.00 | 0.0668 | 280 B |
| GetLengthDivisionBenchmark | 12345(...)12345 [40] | 1,900.12 ns | 37.730 ns | 33.446 ns | 1,896.37 ns | 11.76 | 0.24 | 0.2956 | 1,240 B |
| GetLengthMultiplicationBenchmark | 12345(...)12345 [40] | 1,399.98 ns | 27.838 ns | 77.602 ns | 1,370.01 ns | 9.27 | 0.28 | 0.5569 | 2,336 B |
| GetLengthAbsPowBenchmark | 12345(...)12345 [40] | 12,315.16 ns | 143.022 ns | 111.662 ns | 12,321.32 ns | 76.22 | 0.98 | 3.4637 | 14,520 B |
| BigIntegerLog | 12345(...)12345 [40] | 59.83 ns | 2.957 ns | 8.625 ns | 57.83 ns | 0.34 | 0.02 | - | - |
| CountDigitsBenchmark | 12345(...)12345 [40] | 1,087.25 ns | 18.482 ns | 17.288 ns | 1,086.55 ns | 6.74 | 0.11 | 0.1678 | 704 B |
| ToStringBenchmark | 12345(...)12345 [50] | 197.47 ns | 1.815 ns | 1.417 ns | 197.59 ns | 1.00 | 0.00 | 0.0763 | 320 B |
| GetLengthDivisionBenchmark | 12345(...)12345 [50] | 2,666.97 ns | 22.475 ns | 21.023 ns | 2,665.74 ns | 13.51 | 0.16 | 0.4196 | 1,768 B |
| GetLengthMultiplicationBenchmark | 12345(...)12345 [50] | 1,750.60 ns | 17.269 ns | 13.483 ns | 1,749.85 ns | 8.87 | 0.11 | 0.7782 | 3,256 B |
| GetLengthAbsPowBenchmark | 12345(...)12345 [50] | 15,840.75 ns | 315.818 ns | 569.485 ns | 15,549.61 ns | 79.38 | 2.94 | 5.0964 | 21,360 B |
| BigIntegerLog | 12345(...)12345 [50] | 44.87 ns | 0.809 ns | 0.756 ns | 45.09 ns | 0.23 | 0.00 | - | - |
| CountDigitsBenchmark | 12345(...)12345 [50] | 1,626.71 ns | 27.600 ns | 23.047 ns | 1,623.62 ns | 8.24 | 0.14 | 0.2747 | 1,152 B |
| ToStringBenchmark | 12345(...)12345 [75] | 306.08 ns | 4.371 ns | 3.650 ns | 305.57 ns | 1.00 | 0.00 | 0.1030 | 432 B |
| GetLengthDivisionBenchmark | 12345(...)12345 [75] | 5,192.75 ns | 34.686 ns | 30.749 ns | 5,195.60 ns | 16.96 | 0.17 | 0.7629 | 3,208 B |
| GetLengthMultiplicationBenchmark | 12345(...)12345 [75] | 3,988.09 ns | 271.305 ns | 799.948 ns | 3,794.99 ns | 10.89 | 2.50 | 1.4191 | 5,944 B |
| GetLengthAbsPowBenchmark | 12345(...)12345 [75] | 33,948.30 ns | 1,493.620 ns | 4,403.973 ns | 32,639.63 ns | 132.92 | 8.45 | 10.4370 | 43,848 B |
| BigIntegerLog | 12345(...)12345 [75] | 43.95 ns | 0.908 ns | 1.360 ns | 43.35 ns | 0.14 | 0.00 | - | - |
| CountDigitsBenchmark | 12345(...)12345 [75] | 3,529.34 ns | 68.576 ns | 60.791 ns | 3,531.11 ns | 11.54 | 0.20 | 0.5836 | 2,456 B |
| ToStringBenchmark | 1234(...)2345 [100] | 552.12 ns | 32.468 ns | 95.732 ns | 533.47 ns | 1.00 | 0.00 | 0.1316 | 552 B |
| GetLengthDivisionBenchmark | 1234(...)2345 [100] | 9,353.61 ns | 278.178 ns | 820.215 ns | 9,213.45 ns | 17.62 | 4.21 | 1.1902 | 5,000 B |
| GetLengthMultiplicationBenchmark | 1234(...)2345 [100] | 3,949.08 ns | 49.055 ns | 45.886 ns | 3,945.01 ns | 8.32 | 1.34 | 2.1667 | 9,064 B |
| GetLengthAbsPowBenchmark | 1234(...)2345 [100] | 40,856.02 ns | 442.861 ns | 414.252 ns | 40,816.28 ns | 86.03 | 13.74 | 17.7002 | 74,120 B |
| BigIntegerLog | 1234(...)2345 [100] | 42.35 ns | 0.558 ns | 0.436 ns | 42.26 ns | 0.09 | 0.02 | - | - |
| CountDigitsBenchmark | 1234(...)2345 [100] | 6,511.54 ns | 60.303 ns | 56.407 ns | 6,513.08 ns | 13.70 | 2.11 | 0.9766 | 4,112 B |
| ToStringBenchmark | 1234(...)2345 [150] | 734.17 ns | 11.671 ns | 9.746 ns | 735.48 ns | 1.00 | 0.00 | 0.1831 | 768 B |
| GetLengthDivisionBenchmark | 1234(...)2345 [150] | 18,963.26 ns | 291.798 ns | 272.948 ns | 18,927.82 ns | 25.76 | 0.43 | 2.2278 | 9,384 B |
| GetLengthMultiplicationBenchmark | 1234(...)2345 [150] | 7,402.45 ns | 146.064 ns | 326.694 ns | 7,373.84 ns | 9.63 | 0.46 | 4.0283 | 16,848 B |
| GetLengthAbsPowBenchmark | 1234(...)2345 [150] | 96,553.68 ns | 3,203.319 ns | 9,344.232 ns | 94,618.21 ns | 124.75 | 3.00 | 37.7197 | 157,928 B |
| BigIntegerLog | 1234(...)2345 [150] | 43.73 ns | 0.847 ns | 0.792 ns | 43.57 ns | 0.06 | 0.00 | - | - |
| CountDigitsBenchmark | 1234(...)2345 [150] | 13,799.37 ns | 181.226 ns | 169.519 ns | 13,831.45 ns | 18.75 | 0.27 | 1.9531 | 8,184 B |
| ToStringBenchmark | 1234(...)2345 [200] | 1,170.38 ns | 22.340 ns | 18.655 ns | 1,167.00 ns | 1.00 | 0.00 | 0.2365 | 992 B |
| GetLengthDivisionBenchmark | 1234(...)2345 [200] | 30,656.86 ns | 493.053 ns | 437.079 ns | 30,659.95 ns | 26.21 | 0.70 | 3.5400 | 14,896 B |
| GetLengthMultiplicationBenchmark | 1234(...)2345 [200] | 9,459.47 ns | 115.420 ns | 102.317 ns | 9,419.28 ns | 8.09 | 0.17 | 6.3477 | 26,600 B |
| GetLengthAbsPowBenchmark | 1234(...)2345 [200] | 124,083.76 ns | 2,093.310 ns | 1,748.008 ns | 124,681.07 ns | 106.03 | 1.39 | 65.1855 | 272,776 B |
| BigIntegerLog | 1234(...)2345 [200] | 50.15 ns | 1.029 ns | 1.338 ns | 49.84 ns | 0.04 | 0.00 | - | - |
| CountDigitsBenchmark | 1234(...)2345 [200] | 26,047.64 ns | 520.981 ns | 1,452.286 ns | 25,753.68 ns | 24.32 | 0.90 | 3.2043 | 13,416 B |
CodePudding user response:
There's this:
static int GetLength(this BigInteger value)
{
int result = 1;
while (value >= 10)
{
result ;
value /= 10;
}
return result;
}
I know it seems like the loop could be slow, but it's still probably faster than ToString(), which thanks to localization/cultural issues is probably a LOT slower even than you'd expect.
Or we can invert it to use multiplication and count up, which might be faster depending on the instruction set of the computer, even though it needs an additional variable:
static int GetLength(this BigInteger value)
{
BigInteger power = 10;
int result = 1;
while (power < value)
{
result ;
power *= 10;
}
return result;
}
Finally, I need to point out both of these assume positive values. I feel this is justified, because the original ToString() code would also return a count including the negative sign which is system dependent.
Windows lets me set the default negative sign to be any arbitrary string I want, and someone else logged into a different profile on the same computer could have a completely different setting here (thankfully, people hardly ever change this). The UI limits the number of characters you can use, but the registry location it writes to is much more forgiving for long negative strings.
Therefore, if the original code is allowed to be wrong for negative values, this code can to (and this is much easier to fix).
CodePudding user response:
DO NOT USE THIS!
Check the benchmarks produced by @David L - it's the worst performing.
Many thanks to @Joel Coehoorn, from whose answer I managed to derive this:
static int GetLength(BigInteger value)
{
int result = 1;
BigInteger ten = new(10);
BigInteger absValue = BigInteger.Abs(value);
while(BigInteger.Pow(ten, result) < absValue)
{
result ;
}
return result;
}
Leaving it here for feedback (again, don't use it!)
A Better Solution
As Log10 seems to be the fastest solution, but requires rounding, I've tested the following solution over 50,000 BigInteger values:
static int GetLength(BigInteger value)
{
double log10 = BigInteger.Log10(value);
return (int) Math.Ceiling(log10) 1;
}